17 sie 19:23
a7: co najmniej 35
17 sie 19:51
irek: chodzi o dokładną liczbę
17 sie 19:54
a7:
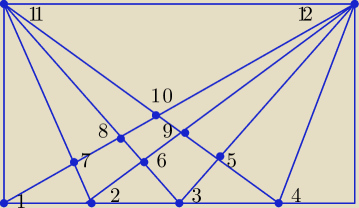
Trójkaty:
(1 2 7) (2 3 6) (3 4 5)
(2 4 9) (1 2 8)
(1, 4, 10)
(1 2 11) (2 3 11) (3 4 11) (1 2 12) (2 3 12) (3 4 12)
(1 3 11) (2 4 11) (2 4 12) (1 3 12)
(1 4 11) (1 4 12)
(10 11 12)
(1 7 11) (7 8 11) (8 9 10) (4 5 12) (5 9 12) (9 10 12)
(1 8 11) (7 10 11) (4 9 12) (5 10 12)
(1 10 11) (4 10 12)
(2 6 11) (6 9 11) (2 9 11) (3 6 12) (6 8 12) (3 8 12)
37 trójkatów
17 sie 20:03
a7: przepraszam jeszcze są
17 sie 20:03
irek: Tam są 4 na 4 a ty masz 3 na 4
17 sie 20:07
a7: jeszcze są z punktem w dolnym prawym rogu (13)
(4 13 12)
(3 13 12)
(2 13 12)
(1 13 12)
(1 13 11)
(2 13 11)
(3 13 11)
(4 13 11)
oraz kolejnych co najmniej 10, spróbuj znaleźć sam
17 sie 20:13
a7: no to może zrób prawidłowy rysunek tutaj taki jak ja tylko z brakująca kreską i oznaczonym
punktem (13) i policzymy wspólnie
17 sie 20:14
irek: Twój rysunek jest prawie ok tylko że powinien być symetryczny.
17 sie 20:19
17 sie 20:31
a7: jeszcze 13 w dolnym rogu
17 sie 20:40
a7:
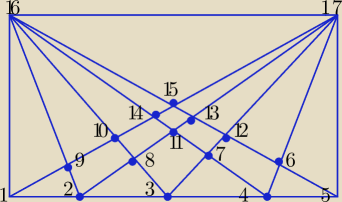
17 sie 20:45
wredulus_pospolitus:
29*2 + 10 + 15 = 83, tyle znalazłem
17 sie 20:58
a7:
(1 2 9) (2 3 8) (3 4 7) (4 5 6)
(1 3 10 ) (2 4 11) (3 5 12)
(1 4 14) (2 5 13)
(1 5 15)
(15 16 17)
(14 16 17) (13 16 17)
(1016 17) (11 16 17) (13 16 17)
(9 16 17) (8 16 17) (7 16 17) (6 16 17)
(1 16 17) (2 16 17) (3 16 17) (4 16 17) (5 16 17)
(1 2 16) (1 3 16) (1 4 16) (1 5 16)
(5 16 17)
(1 2 17) (1 3 17) (1 4 17) (1 5 17)
(1 16 17)
(1 9 16) (9 10 16) (10 14 16) (14 15 16) ( symetrycznie "od piątki") (5 6 17) (6 12 17) (12 13
17) (13 15 17)
(1 10 16) (1 14 16) ( 1 15 16) (5 12 17) (5 13 17) (5 15 17)
(1 14 16) (1 15 16) (5 13 17) (5 15 17)
to jeszcze nie wszystkie
17 sie 21:02
a7: czyli u mnie brakuje jeszcze 30 (?)
17 sie 21:03
a7:
( 2 8 16) ( 8 11 16) (11 13 16) (11 16 17)
(2 11 160 ( 8 13 16) (2 16 17) (8 16 17)
(4 7 17) (7 11 17) (11 14 17) (13 16 17)
(4 11 17) (7 14 17) (4 14 17) (12 16 17)
(9 16 17) (6 16 17)
tu jest jeszcze 18
(zostało do wypisania jeszcze 12)
17 sie 21:14
wredulus_pospolitus:
@a7:
trójkąty typu (16,17,x) jest ich 15 (je rozpatrujesz)
trójkąty bez 16 i 17 −−− jest ich 10 (je rozpatrujesz)
trójkąty z 16, ale bez 17 (oraz tylko z 17, ale bez 16 jest tyle samo), tych mi wyszło po 29:
16 będę pomijał:
'pojedyncze'
1,2 ; 1,9
9,10 ; 2,8 ; 2,3
10,14 ; 8,11 ; 3,7 ; 3,4
14,15 ; 11,13 ; 7,12 ; 4,6 ; 4,5
'podwójne'
1,10 ; 1,3
9,14 ; 2,11 ; 2,4
10,15 ; 8,13 ; 3,12 ; 3,5
'potrójne'
1,14 ; 1,4
9,15 ; 2,13 ; 2,5
'poczwórne'
1,15 ; 1,5
co daje nam 30 (no to jednego wcześniej nawet nie policzyłem)
i to *2, bo zamiast wierzchołka 16 robimy wierzchołek 17.
no to mamy 85 sztuk
17 sie 21:15
a7:
(2 9 17) (8 10 17) (11 14 17) ( 13 15 17)
(4 6 16) (7 12 16) (11 13 16)
no i jeszcze 5 do wypisania (?)
@ Irek widzisz już jak trzeba patrzeć czy czekasz na gotowca?
17 sie 21:19
a7: czyli jeszcze 7 do wypisania @Irek spróbuj!
17 sie 21:20
irek: Popróbuję choć nie wiem czy mi się uda
17 sie 21:23
a7: ok, daj znać, jakby co to ja jeszcze pomyślę
17 sie 21:24
irek: W sumie ma ich być 85

17 sie 21:25
a7:
(3, 16, 17) (11, 16, 17)
17 sie 21:26
a7: najprawdopodobniej tak (85)
17 sie 21:26
a7:
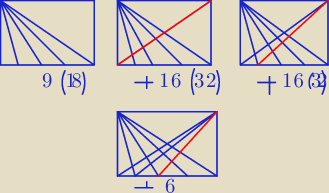
wyszło mi 88
17 sie 23:39
wredulus_pospolitus:
@a7 − wyjaśnij metodologię związaną z tymi rysunkami
co oznaczają czerwone odcinki?
18 sie 00:09
wredulus_pospolitus: I jak się one mają do liczby trójkątów w danej opcji
18 sie 00:09
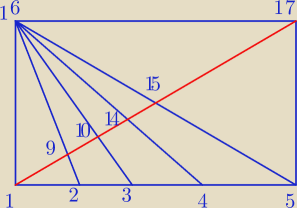
a7: na pierwszym rysunku mamy 9 trójkatów i symtrycznie byloby kolejne 9 dla kresek z drugiej
strony
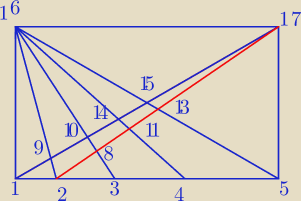
na drugim rysunku policzylam ile trójkątów dochodzi do tych 9(18) gdy dorysujemy tę czerwoną
linię wyszło mi 16 (symetrycznie będzie drugei 16) czyli w sumie 32
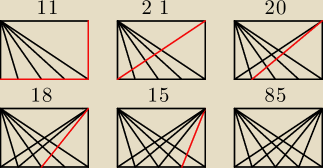
na trzecim rysunku to samo, co na drugim tylko dla lini nr 2 i kolejne 16 932 trójkąty i
właśnie widzę, że rysunek czwarty jeszcze muszę zweryfikować
18 sie 00:18
a7: bo albo powinien być piąty, ale przemyślany, albo w ogóle ta metoda jest nie całkiem dobra
18 sie 00:20
wredulus_pospolitus:
@a7 ... jeszcze raz napiszę:
1) jaki jest związek pomiędzy ilością trójkątów na drugim obrazku z czerwoną linią? Jakie
trójkąty bierzesz tam pod uwagę a jakich NIE BIERZESZ pod uwagę?
Co musi być spełnione, aby brać pod uwagę dany trójkąt (w danym przypadku) jako trójkąt który
wliczasz do danego przypadku?
18 sie 00:21
a7: na trzecim rysunku kolejne 16 (32) trójkątów
18 sie 00:22
a7: na drogim rysunku już nie uwzględniamy trójkątów z pierwszego rysunku na trzecim z pierwszego i
drugiego, na czwartym z pierwszego, drugiego i trzeciego ( a na piątym, którego nie ma,a chyba
powinien być analogicznie j.w.)
18 sie 00:23
wredulus_pospolitus:
zacznijmy od tego, że:
ewentualny błąd 1: mnożąc przez 2 zliczasz wielokrotnie te same trójkąty (chociaż nie wiem jak
dokładnie je zliczasz)
ewentualny błąd 2: błędne ilości trójkątów podajesz (albo po prostu ja nie rozumiem na jakiej
zasadzie np. w drugim przypadku masz 16 trójkątów * 2)
18 sie 00:24
wredulus_pospolitus:
czyli innymi słowy −−− liczysz tylko te trójkąty, których jeden z boków zawiera się z czerwoną
linią ... zgadza się

18 sie 00:25
a7: zaraz to mogę lepiej rozpisać t.j. rysunek 1 i 2
18 sie 00:25
a7: chyba jest dobrze i jest jeszcze więcej trójkątów
18 sie 00:25
a7:
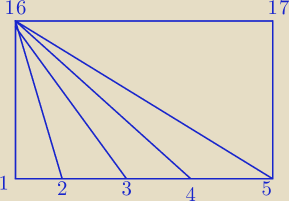
(1 2 16) (2 3 16) (3 4 16) (4 5 16)
(1 3 16) (2 4 16) (3 5 16)
(1 4 16) (2 5 16)
(1 5 16) (5 16 17)
11 trójkątów
zgadza się?
18 sie 00:30
a7: 00:25 nie
18 sie 00:30
wredulus_pospolitus:
tak ... 11 trójkątów jest w pierwszym
18 sie 00:31
wredulus_pospolitus:
rozpisz mi drugi rysunek
18 sie 00:32
wredulus_pospolitus:
ale co "00:25 nie"

różnica pomiędzy 1 a 2 rysunkiem to dorysowanie odcinka czerwonego ... więc skoro zliczasz
trójkąty których wcześniej nie liczyłaś, to znaczy że zliczasz w następnym kroku te trójkąty
które powstają dzięki temu, że jednym z ich boków jest jakaś część dorysowanego odcinka
(czerwonego)
18 sie 00:34
a7:
(1 2 9) (1 3 10) (1 4 14) (1 5 15)
(1 9 16) (9 10 16) (10 14 16) (14 15 16) (15 16 17)
(5 15 17)
(1 10 16) (9 14 16) (14 16 17)
(1 14 16) (9 15 16) (10 16 17)
(1 15 16) (9 16 17)
(1 5 17) (1 16 17)
+20 trójkątów zgadza się?
(symetrycznie będzie drugie 20 ?)
18 sie 00:38
a7: 00:25 , 00:38 jednak tak , racja
18 sie 00:39
a7: acha symetrycznie nie będzie drugie 20 ....
18 sie 00:40
wredulus_pospolitus:
oczywiście że nie będzie bo:
1) dwukrotnie liczysz (15,16,17)
2) dodatkowo(1,5,17) symetryczny liczysz w pierwszym rysunku jako (5,1,16)

I później błędy się tylko powielają
18 sie 00:41
a7: po prostu +20
18 sie 00:42
wredulus_pospolitus:
I jak dla mnie − drugi rysunek to 21 trójkątów:
'górna część przekątnej'
pojedyncze:
1,9,16 ; 9,10,16 ; 10,14,16 ; 14,15,16 ; 15,17,16
podwójne:
1,10,16 ; 9,14,16 ; 10,15,16 ; 14,17,16
potrójne:
1,14,16 ; 9,15,16 ; 10,17,16
poczwórne:
1,15,16 ; 9,17,16
oraz:
1,17,16
dolna część przekątnej:
1,9,2 ; 1,10,3 ; 1,14,4 ; 1,15,5 ; 1,17,5 ; 15,17,5
co daje nam:
| | 6 | |
5+4+3+2+1 + 6 = |
| *5 + 6 = 21 |
| | 2 | |
18 sie 00:46
wredulus_pospolitus:
w pozostałych rysunkach także nie podobają mi się ilości trójkątów
18 sie 00:46
a7:
(2 8 16) (8 11 16) (11 13 16) (2 11 16) (8 13 16) (11 16 17)
(13 15 17) (5 13 17) (11 1417) (13 16 17) (11 16 17) (8 10 17) (11 13 16)
(8 10 17) (8 11 16)
(2 9 17) (2 13 16) (2 16 17) (2 5 17)
(1 2 17)
+20 trójkatów
18 sie 00:50
a7: 00:46 racja
18 sie 00:52
a7: jeszcze (13 16 17)
czyli +21 trójkątów zgadza się?
18 sie 00:55
wredulus_pospolitus:
Moja propozycja:
przynajmniej jakaś część czerwonego odcinka musi być bokiem rozpatrywanego trójkąta (w danym
przypadku)
18 sie 00:57
wredulus_pospolitus: ((13 16 17) już wliczałaś −−−
(2 8 16) (8 11 16) (11 13 16) (2 11 16) (8 13 16) (11 16 17)
(13 15 17) (5 13 17) (11 1417) (13 16 17) (11 16 17) (8 10 17) (11 13 16)
(8 10 17) (8 11 16)
(2 9 17) (2 13 16) (2 16 17) (2 5 17)
18 sie 00:59
a7:
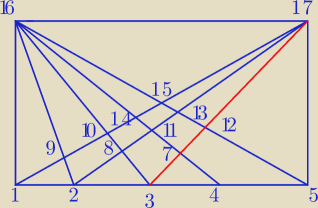
(3 7 16) (7 12 16) (12 16 17)(12 13 17) (12 15 17) (12 16 17)
(7 11 17) (7 14 17)(7 12 16) (5 12 17)
(3 4 7) (3 5 12) (3 5 17)
(3 12 16) (3 16 17)
+ 15 trójkątów (?)
18 sie 01:02
a7: ok, wygląda na to, że masz i tu rację
18 sie 01:03
a7: ale fajne to zadanko
18 sie 01:04
wredulus_pospolitus:
pojedyncze
(3 7 16) (7 12 16) (12 16 17)
podwójne:
(3 12 16)
(7,16,17)
potrójny:
(3 16 17)
małe:
(12 13 17) (7 11 17)
(3 8 17)
większe:
(3 10 17) (7 14 17) (12 15 17)
dolna część:
(5 12 17) (3 4 7) (3 5 12) (3 5 17)
18 sztuk jak dla mnie (pozwoliłem sobie podzielić 'po swojemu'

, mam nadzieję, że widzisz
algorytm)
18 sie 01:07
wredulus_pospolitus:
coś mi nie pasuje.
Ty policzyłaś dwukrotnie (7 12 16) oraz (12 16 17)
(3 7 16)
(7 12 16) (12 16 17) (12 13 17) (12 15 17)
(12 16 17)
(7 11 17) (7 14 17)
(7 12 16) (5 12 17)
(3 4 7) (3 5 12) (3 5 17)
(3 12 16) (3 16 17)
Dlatego po znalezieniu trzech, których nie masz przerwałem ... a tak naprawdę wypisałem tylko
16 trójkątów.
są jeszcze dwa:
[Z[rozwartokątne

]
(1 3 17) (2 3 17)

I teraz (z tymi co podałem wcześniej) mamy 18 trójkątów
18 sie 01:18
a7: ok


18 sie 01:34
I'm back:
To jeszcze 'na dobranoc' załatw ostatni przypadek i ostatnie 15 trójkątów

18 sie 01:38
a7:
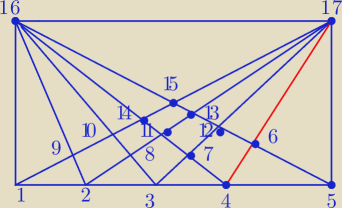
(4 5 6) (5 6 17) (4 5 16) (6 12 17) (6 13 17) (6 15 17) (6 16 17)
(4 6 16) (4 16 17)
widzę te 9 i idę spać...
18 sie 02:01
wredulus_pospolitus:
rozwartokątne:
(1 4 17) , (2 4 17) , (3 4 17)
nie (4 5 16) tylko (4 5 1
7)
masz (6 x 17) a nie zrobiłaś (4 x 17) czyli (4 7 17) , (4 11 17) , (4 14 17)
i to daje nam w sumie z Twoimi 9'cioma dokładnie 15

18 sie 02:06
a7: 
18 sie 09:42
 Trójkaty:
(1 2 7) (2 3 6) (3 4 5)
(2 4 9) (1 2 8)
(1, 4, 10)
(1 2 11) (2 3 11) (3 4 11) (1 2 12) (2 3 12) (3 4 12)
(1 3 11) (2 4 11) (2 4 12) (1 3 12)
(1 4 11) (1 4 12)
(10 11 12)
(1 7 11) (7 8 11) (8 9 10) (4 5 12) (5 9 12) (9 10 12)
(1 8 11) (7 10 11) (4 9 12) (5 10 12)
(1 10 11) (4 10 12)
(2 6 11) (6 9 11) (2 9 11) (3 6 12) (6 8 12) (3 8 12)
37 trójkatów
Trójkaty:
(1 2 7) (2 3 6) (3 4 5)
(2 4 9) (1 2 8)
(1, 4, 10)
(1 2 11) (2 3 11) (3 4 11) (1 2 12) (2 3 12) (3 4 12)
(1 3 11) (2 4 11) (2 4 12) (1 3 12)
(1 4 11) (1 4 12)
(10 11 12)
(1 7 11) (7 8 11) (8 9 10) (4 5 12) (5 9 12) (9 10 12)
(1 8 11) (7 10 11) (4 9 12) (5 10 12)
(1 10 11) (4 10 12)
(2 6 11) (6 9 11) (2 9 11) (3 6 12) (6 8 12) (3 8 12)
37 trójkatów


 wyszło mi 88
wyszło mi 88

 (1 2 16) (2 3 16) (3 4 16) (4 5 16)
(1 3 16) (2 4 16) (3 5 16)
(1 4 16) (2 5 16)
(1 5 16) (5 16 17)
11 trójkątów
zgadza się?
(1 2 16) (2 3 16) (3 4 16) (4 5 16)
(1 3 16) (2 4 16) (3 5 16)
(1 4 16) (2 5 16)
(1 5 16) (5 16 17)
11 trójkątów
zgadza się?
 różnica pomiędzy 1 a 2 rysunkiem to dorysowanie odcinka czerwonego ... więc skoro zliczasz
trójkąty których wcześniej nie liczyłaś, to znaczy że zliczasz w następnym kroku te trójkąty
które powstają dzięki temu, że jednym z ich boków jest jakaś część dorysowanego odcinka
(czerwonego)
różnica pomiędzy 1 a 2 rysunkiem to dorysowanie odcinka czerwonego ... więc skoro zliczasz
trójkąty których wcześniej nie liczyłaś, to znaczy że zliczasz w następnym kroku te trójkąty
które powstają dzięki temu, że jednym z ich boków jest jakaś część dorysowanego odcinka
(czerwonego)
 (1 2 9) (1 3 10) (1 4 14) (1 5 15)
(1 9 16) (9 10 16) (10 14 16) (14 15 16) (15 16 17)
(5 15 17)
(1 10 16) (9 14 16) (14 16 17)
(1 14 16) (9 15 16) (10 16 17)
(1 15 16) (9 16 17)
(1 5 17) (1 16 17)
+20 trójkątów zgadza się?
(symetrycznie będzie drugie 20 ?)
(1 2 9) (1 3 10) (1 4 14) (1 5 15)
(1 9 16) (9 10 16) (10 14 16) (14 15 16) (15 16 17)
(5 15 17)
(1 10 16) (9 14 16) (14 16 17)
(1 14 16) (9 15 16) (10 16 17)
(1 15 16) (9 16 17)
(1 5 17) (1 16 17)
+20 trójkątów zgadza się?
(symetrycznie będzie drugie 20 ?)
 I później błędy się tylko powielają
I później błędy się tylko powielają
 (2 8 16) (8 11 16) (11 13 16) (2 11 16) (8 13 16) (11 16 17)
(13 15 17) (5 13 17) (11 1417) (13 16 17) (11 16 17) (8 10 17) (11 13 16)
(8 10 17) (8 11 16)
(2 9 17) (2 13 16) (2 16 17) (2 5 17)
(1 2 17)
+20 trójkatów
(2 8 16) (8 11 16) (11 13 16) (2 11 16) (8 13 16) (11 16 17)
(13 15 17) (5 13 17) (11 1417) (13 16 17) (11 16 17) (8 10 17) (11 13 16)
(8 10 17) (8 11 16)
(2 9 17) (2 13 16) (2 16 17) (2 5 17)
(1 2 17)
+20 trójkatów
 Moja propozycja:
przynajmniej jakaś część czerwonego odcinka musi być bokiem rozpatrywanego trójkąta (w danym
przypadku)
Moja propozycja:
przynajmniej jakaś część czerwonego odcinka musi być bokiem rozpatrywanego trójkąta (w danym
przypadku)
 (3 7 16) (7 12 16) (12 16 17)(12 13 17) (12 15 17) (12 16 17)
(7 11 17) (7 14 17)(7 12 16) (5 12 17)
(3 4 7) (3 5 12) (3 5 17)
(3 12 16) (3 16 17)
+ 15 trójkątów (?)
(3 7 16) (7 12 16) (12 16 17)(12 13 17) (12 15 17) (12 16 17)
(7 11 17) (7 14 17)(7 12 16) (5 12 17)
(3 4 7) (3 5 12) (3 5 17)
(3 12 16) (3 16 17)
+ 15 trójkątów (?)
 , mam nadzieję, że widzisz
algorytm)
, mam nadzieję, że widzisz
algorytm)
 ]
(1 3 17) (2 3 17)
]
(1 3 17) (2 3 17)  I teraz (z tymi co podałem wcześniej) mamy 18 trójkątów
I teraz (z tymi co podałem wcześniej) mamy 18 trójkątów



 (4 5 6) (5 6 17) (4 5 16) (6 12 17) (6 13 17) (6 15 17) (6 16 17)
(4 6 16) (4 16 17)
widzę te 9 i idę spać...
(4 5 6) (5 6 17) (4 5 16) (6 12 17) (6 13 17) (6 15 17) (6 16 17)
(4 6 16) (4 16 17)
widzę te 9 i idę spać...

