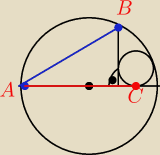
okręgi styczne w18: Wykorzystując dane z rysunku oblicz stosunek AB/AC.

kerajs: Skoro wskazane boki są równe to ich stosunek wynosi 1.

w18: Czemu te boki są równe?

kerajs: Niech większy okrąg ma środek O i promień R. Ponadto kąt ostry BAC nazwę α, więc kąt BOC to 2α. |AB| = 2Rcosα Z tw. Pitagorasa wyliczam r (promień mniejszego okręgu) jako funkcję R i α : (Rcos2α+r)²+r²=(R−r)² r²+2R(cos2α+1)r−Rsin²2α=0 Δ=16R²cos²α ⇒ r=2R(−cos²α+cosα) |AC|=R+Rcos2α+r=R+R(2cos²α−1)+2R(−cos²α+cosα)=2Rcosα=|AB|

wredulus_pospolitus: Skąd to powstało ? (Rcos2α+r)²+r²=(R−r)²

kerajs: A tyle razy sobie obiecywałem nie wypowiadać się w tematach, gdzie edycja rozwiązania jest kilkukrotnie dłuższa od samego rozwiązania! Środek mniejszego okręgu oznaczam przez Q, a rzuty punktów B i Q na podstawę półokręgu przez B' i Q' Równanie (Rcos2α+r)²+r²=(R−r)² to tw. Pitagorasa w trójkącie OQQ'. Odpowiada mu zapis: (|OB'|+|B'Q'|)²+|QQ'|²=(|OQ|)²