Dowody Bill: Witam, mam takie zadanka z dowodów: 1. Podstawy trapezu mają miary 20 i 16, oblicz długość odcinka c równoległego do podstaw trapezu i zawierającego punkt przecięcia jego prostokątnych. 2. Dane są boki A i B trójkąta ABC, znajdź bok c, jeżeli wiadomo, że kąt przy wierzchołku c jest 2 razy większy od kąta przy wierzchołku b. 3. Dane są wysokości trójkąta ha=1/3m, hb=1/4m i hc=1/5m. Znajdź boki i pole trójkąta. Ktoś ma jakiś pomysł, jak za to się zabrac? Co powinienem przeczytać żeby umiec to zrobic? W moim podręczniku dowody geometryczne są opisane niesamowicie ogólnikowo, zaś z tego miałem zaledwie jedną lekcję, i już niby mam to umiec...

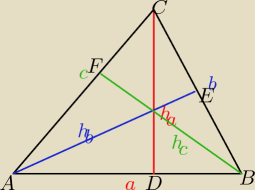
Basia: a*h_a=b*h_b=c*h_c ^a₃=^b₄=^c₅ b = ^4a₃ c=^5a₃ teraz stosujemy wzór Herona na pole trójkąta https://matematykaszkolna.pl/strona/503.html

	a+b+c		a+4a3+5a3
p=		=		=
	2		2

3a+4a+5a		12a
	=		=2a
6		6

p−a=a p−b=a−^4a₃=−¹₃a p−c=a−^5a₃=−²₃a

	2a2
P=√2a*a*(−13a)*(−23a) = √4a49 =
	3

P= ¹₂a*h_a=¹₆a

2a2		a
	=		/*6
3		6

4a²=a 4a²−a=0 a(4a−1)=0 a≠0 4a−1=0 a=¹₄ b=⁴₃*¹₄ = ¹₃ c=⁵₃*¹₄ =⁵₁₂ P=¹₂*¹₄*¹₃ = ¹₂₄

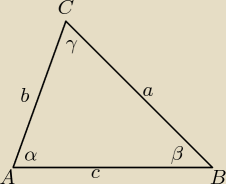
Basia: dane: a,b γ=2β α=180−β−γ=180−3β z tw.sinusów

sinα		sinβ		sinγ
	=		=
a		b		c

sin(180−3β)		sinβ		sin2β
	=		=
a		b		c

sin3β		sinβ
	=
a		b

sin3β		a
	=
sinβ		b

sin3β=sin(β+2β}=sinβcos2β+sin2βcosβ= sinβ(1−2sin²β)+2sinβcosβ*cosβ= sinβ[1−2sin²β+cos²β]= sinβ[1−2sin²β+1−sin²β]= sinβ[2−3sin²β] stąd:

	a
2−3sin2β=
	b

	a
3sin2β=2−
	b

	2b−a
3sin2β=
	b

	2b−a
sin2β=
	3b

	2b−a		3b−2b+a		a+b
cos2β=1−		=		=
	3b		3b		3b

	2b−a
sinβ=√
	3b

	a+b
cosβ=√
	3b

	2b−a)(a+b)		√(2b−a)(a+b)
sin2β=2sinβcosβ=√		=
	9b2		3b

sinβ		sin2β
	=
b		c

c*sinβ=b*sin2β

	b*sin2β
c=
	sinβ

teraz trzeba podstawić wyliczone sinβ i sin 2β i wyliczyć c w zależności od a,b

Basia: Zadanie 2 można rozwiązać także inaczej, ale zawsze będzie trzeba policzyć sinβ.lun cosβ sposób 2

	1		a*b*sin2β
P=		a*b*sinγ=
	2		2

	1
P=		a*c*sinβ
	2

stąd a*b*sin2β=a*c*sinβ

	b*sin2β		2b*sinβ*cosβ
c=		=		= 2b*cosβ
	sinβ		sinβ

cosβ wyliczasz jak w rozwiązaniu 1 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− sposób 3 c² = a²+b²−2ab*cosγ c² = a²+b²−2abcos2β c² = a²+b²−2ab(cos^β−sin²β) sinβ i cosβ wyliczasz jak w rozwiązaniu 1

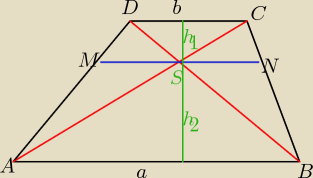
Basia: a=20 b=16 tr.ASB ∼ tr.CSD w skali s=^a_b ⇒

h2		a
	=
h1		b

	ah1
h2=
	b

	a+b		a+b
PABCD=		*h =		*(h1+h2)
	2		2

	a+c
PABNM=		*h2
	2

	c+b
PMNCD=		*h1
	2

stąd (a+b)(h₁+h₂) = (a+c)*h₂+(c+b)*h₁ (a+b)(h₁+h₂)=a*h₂+c*h₂+c*h₁+b*h₁ a*h₁+a*h₂+b*h₁+b*h₂ = a*h₂+c(h₁+h₂)+b*h₁ a*h₁+b*h₂ = c(h₁+h₂)

	ah1		ah1
a*h1+b*		= c(h1+		)
	b		b

	b*h1+a*h1
a*h1+a*h1 = c(
	b

	h1(a+b)
2a*h1 = c*		/:h1
	b

	a+b
2a = c*
	b

	2ab
c =
	a+b

Basia: Na pytanie co musisz umieć odpowiedź jest bardzo krótka: wszystko co związane z wzorami na pola figur + trygonometria + związki trygonometrii z figurami, głownie z trójkatem + podobieństwo czyli tak na prawdę całą planimetrię i trygonometrię

Bill: Dziękuję bardzo za pomoc, na weekend wezmę się do pracy