Niewymierność wymierna Ciufcia: Witam, poszukuje pomocy w rozwiązaniu tego zadania z 18. Dla jakich wartości parametru m nierówność jest prawdziwa dla kazdego x∊R.

(m − 3)x+3
	> −2
−x2 + x −2

Ciufcia: Jak na razie przeniosłem −2 na lewą stronę i dodałem do ułamka wyszło mi:

−2x2 + xm −x −1
	> 0
−x2 + x − 2

ICSP: Określona jest dla każdego x ∊ R. Mnożąc przez (−1)

(m−3)x + 3
	< 2
x2 − x + 2

(m−3)x + 3 < 2x² − 2x + 4 2x² + (1−m)x + 1 > 0 dla każdego x, więc wystarczy sprawdzić kiedy Δ < 0.

ICSP:

−2x2 + xm − x − 1
	> 0
−x2 + x − 2

mianownik jest ujemny dla każdego x, więc aby ułamek był zawsze dodatni to licznik musi być zawsze ujemny: −2x² + xm − x − 1 < 0 2x² + (1−m)x + 1 > 0 dalej wniosek jak w moim powyższym poście.

Ciufcia: Ooo dziękuję bardzo. Teraz już chyba rozumiem

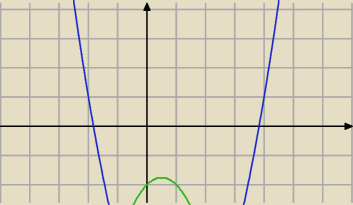
a7: mianownik różny od zera (Δ<0) mianownik jest mniejszy od zera czyli mnożymy ze zmianą znaku (m−3)x+3<−2(−x²+x−2) 2x²−2x−(m−3)x+1>0 2x²+x(1−m)+1>0 Δ musi być<0 Δ=(1−m)²−8 m²−2m−7<0 Δ₂=4+28=32 √Δ₂=4√2 m₁=1−2√2 lub m₂=1+2√2 odp. m∊(1−2√2;1+2√2)