kąt
bella: Niech ABC będzie trójkątem w którym kąt CAB= 60o, oraz AD,BE są dwusiecznymi kątów odpowiednio
BAC, ABC, gdzie D∊BC, E∊ AC. Wiedząc że AB+BD=AE+BE oblicz miarę kąta ABC.
6 sie 21:27
a7:
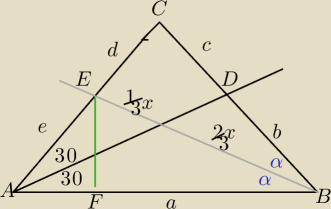
a+b=e+x
z tw. o dwusiecznych dla ΔABE
z tw. Pitagorasa dla ΔBEF
| | e | | e√3 | | e√6 | |
x2=(a− |
| )2+( |
| )2 ⇒x= |
| |
| | 2 | | 2 | | 2 | |
z ΔBEF
| e√3 | | √2 | |
| /x=sinα ⇒ |
| ⇒α=45o ⇒ 2α=∡ABC=90o (?) |
| 2 | | 2 | |
7 sie 02:37
a7: niestety źle
7 sie 02:49
7 sie 09:21
a7: wydaje mi się, że już równanie a+b=x+e jest ok tymczasem w wolframie wychodzi nierealny wynik
x>π
7 sie 09:23
a7: ?
7 sie 09:23
a7: (w Wolframie α=x)
7 sie 09:39
an: Tu nie trzeba żadnych wielkich obliczeń i nie ma potrzeby trudzić wolframa. Kąt wynosi 80o,
zacznij od narysowania trójkąta równobocznego i na nim utwórz trójkąt z zadania,
przeanalizuj powstałe trójkąty równoramienne
7 sie 10:29
a7: Dzień dobry

skąd wiadomo, że ten kąt to 80
o? i co masz na myśli, żeby zbudować/utworzyć trójkąt z zadania
na trójkącie równobocznym i jak przeanalizować powstałe trójkąty, żeby wyszło 80
o?
7 sie 10:34
an: Właśnie z tej analizy arytmetyki oraz sumy kątów w trójkącie.
7 sie 10:36
a7: ju z chyba rozumiem
7 sie 10:41
a7:
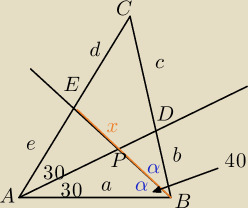
niestety dalej nie rozumiem, gdzie są te trójkąty równoramienne?
7 sie 10:49
an:
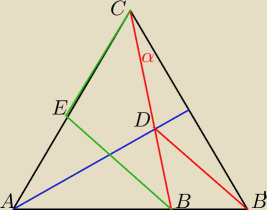
7 sie 10:50
a7:
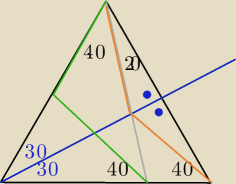
7 sie 11:00
a7: już rozumiem, dzięki serdeczne!
7 sie 11:00
 a+b=e+x
z tw. o dwusiecznych dla ΔABE
a+b=e+x
z tw. o dwusiecznych dla ΔABE
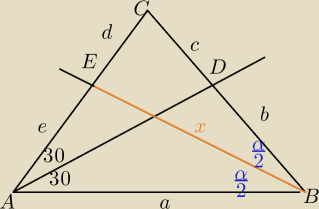 a+b=x+e
z tw. sinusów
dla ΔADB
a+b=x+e
z tw. sinusów
dla ΔADB
 skąd wiadomo, że ten kąt to 80o? i co masz na myśli, żeby zbudować/utworzyć trójkąt z zadania
na trójkącie równobocznym i jak przeanalizować powstałe trójkąty, żeby wyszło 80o?
skąd wiadomo, że ten kąt to 80o? i co masz na myśli, żeby zbudować/utworzyć trójkąt z zadania
na trójkącie równobocznym i jak przeanalizować powstałe trójkąty, żeby wyszło 80o?
 niestety dalej nie rozumiem, gdzie są te trójkąty równoramienne?
niestety dalej nie rozumiem, gdzie są te trójkąty równoramienne?

