trójkąt prostokątny równoramienny
misz:
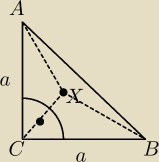
Oblicz pole trójkąta ABC jeśli CX=3, AX=4, BX=5.
6 sie 13:45
wredulus_pospolitus:
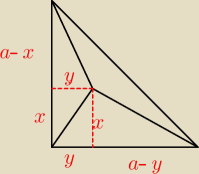
z tw. Pitagorasa:
x
2 + y
2 = 3
2
(a−x)
2 + y
2 = 4
2
(a−y)
2 + x
2 = 5
2
rozwiązujesz ten układ trzech równań w celu wyznaczenia 'a'
a wtedy:
6 sie 15:48
wredulus_pospolitus:
x
2 + y
2 = 3
2
(a−x)
2 + y
2 = 4
2
(a−y)
2 + x
2 = 5
2
x
2 + y
2 = 3
2
(a−x)
2 + 9 − x
2 = 16
(a−y)
2 + 9 − y
2 = 25
x
2 + y
2 = 3
2
a
2 − 2ax = 7
a
2 − 2ay = 16
x
2 + y
2 = 3
2
(a
2−7)
2 + (a
2−16)
2 = 9(2a)
2
(a
2−7)
2 + (a
2−16)
2 = 36a
2
// t = a
2 //
t
2 − 14t + 49 + t
2 − 32t + 256 = 36t
2t
2 − 82t + 305 = 0
Δ = 6
√119
deliberujemy który z tych dwóch wyników odrzucamy (i dlaczego).
I mamy praktycznie pole wyznaczone.
6 sie 15:59
misz: A który odrzucamy? Bo niestety nie wiem
6 sie 17:06
wredulus_pospolitus:
to się zastanów się.
oszacuj ile by wynosiło 'a' w obu przypadkach i popatrz na dane które masz w zadaniu
6 sie 17:43
misz: Skoro tak piszesz to pewnie to mniejsze t

6 sie 17:46
wredulus_pospolitus:
może tak ... może nie ... któż to wie ... pomyślisz chwilę nad tym to się dowiesz, a jak nie
... to nie

6 sie 17:49
misz: Czy musimy sprawdzić to z warunki trójkąta?
6 sie 18:12
wredulus_pospolitus:
Chodzi Ci o nierówności trójkąta

Jeżeli tak to ... yyyy ... nie.
6 sie 18:14
misz: To niestety nie wiem

6 sie 18:19
wredulus_pospolitus:
jak oszacujesz:
...

< t
1 < ...

i wtedy co powiesz o a
1 
i czy widzisz jakiś problem z taką wartością dla boku trójkąta
mając dane długości w treści zadania

6 sie 18:20
misz : No ten duży jest za duży

bo musi być mniejsze od 9

6 sie 18:24
wredulus_pospolitus:
he

| | 82 − 6√119 | | 82 − 6√100 | | 82 − 60 | |
t1 = |
| < |
| = |
| = 5,5 |
| | 4 | | 4 | | 4 | |
więc a
1 <
√5.5 <
√9 = 3
więc a
1 < 3 .... czyli trójkąt ten miałby wtedy przyprostokątne krótsze niż 3 ... jak to się
ma z |CX| = 3

I co to by wtedy oznaczało

6 sie 18:28
wredulus_pospolitus:
Albo co to oznacza patrząc na |AX| bądź |BX|

6 sie 18:33
misz : A nie mozna tego sprawdzić z warunku trójkata AXC?
6 sie 18:33
wredulus_pospolitus:
no i co Ci da sprawdzenie tych warunków ?
a1 < 3+4 = 7 co jest spełnione dla obu przypadków, pozostałe nierówności trójkąta także będą
spełnione
6 sie 18:37
misz : A bo tam trzeba wziąć
√t 
6 sie 18:37
wredulus_pospolitus:
nie jest problemem dla obu a1 i a2 zbudowania trójkątów ABX, ACX, BCX ... problemem jest to,
że w przypadku a1 ... punkt X wypada poza trójkąt, ponieważ:
1) |CX| < a
2) |BX| < a√2
3) |AX| < a√2
tylko wtedy punkt X może (ale nadal NIE MUSI) leżeć wewnątrz trójkąta prostokątnego
równoramiennego o ramieniu 'a'
6 sie 18:39
misz : Czyli jednak to dłuższe t bierzemy bo a musi być wieksze ≥3
6 sie 18:39
wredulus_pospolitus:
a powyższe nierówności (z 18:39) nie są spełnione dla a
1 <
√5.5 
a dwa z nich nie są
spełnione nawet dla mocnego szacowania jakim jest a
1 < 3
6 sie 18:41
wredulus_pospolitus:
| | 5 | |
nawet więcej a > |
| ≈ 3.54 |
| | √2 | |
6 sie 18:42
Mila:
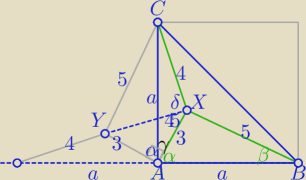
1) α+γ=90
o
2) Po dorysowaniu przystających trójkątów: ( niezbyt dokładny rysunek)
|∡YAX|=90
o
ΔYAX− Δprostokątny równoramienny .
|XY|=3
√2
3)
W ΔCXY:
25=18+16−2*3
√2*4cosδ
| | 3 | | √119 | | √119 | |
cosδ= |
| , sinδ= |
| = |
| |
| | 8√2 | | √128 | | 8√2 | |
4)
|∡AXC|= 45
o+δ
| | √2 | | √2 | |
cos(45o+δ)= |
| cosδ− |
| sinδ |
| | 2 | | 2 | |
| | √2 | | 3 | | √119 | |
cos(45+δ)= |
| *( |
| − |
| ) |
| | 2 | | 8√2 | | 8√2 | |
5)
W ΔAXC:
=============
9 gru 23:10
Mila:
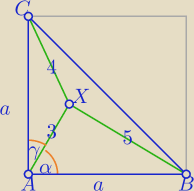
II sposób :
α+γ=90
o
1) W ΔXAB:
| | a2−16 | |
52=32+a2−2a*3cosα ⇔cosα= |
| |
| | 6a | |
2)
W ΔCAX:
| | a2−7 | |
42=a2+32−2a*3cosγ ⇔cosγ= |
| = sinα |
| | 6a | |
3)
sin
2α+cos
2α=1
⇔
2a
4−82a
2+305=0
Δ=6724−2440=4284=36*119
Odrzucamy przypadek z (−) w liczniku
Odp.
===================
10 gru 17:19
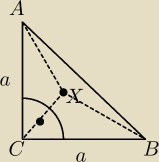 Oblicz pole trójkąta ABC jeśli CX=3, AX=4, BX=5.
Oblicz pole trójkąta ABC jeśli CX=3, AX=4, BX=5.
 z tw. Pitagorasa:
x2 + y2 = 32
(a−x)2 + y2 = 42
(a−y)2 + x2 = 52
rozwiązujesz ten układ trzech równań w celu wyznaczenia 'a'
a wtedy:
z tw. Pitagorasa:
x2 + y2 = 32
(a−x)2 + y2 = 42
(a−y)2 + x2 = 52
rozwiązujesz ten układ trzech równań w celu wyznaczenia 'a'
a wtedy:


 Jeżeli tak to ... yyyy ... nie.
Jeżeli tak to ... yyyy ... nie.

 < t1 < ...
< t1 < ...  i wtedy co powiesz o a1
i wtedy co powiesz o a1  i czy widzisz jakiś problem z taką wartością dla boku trójkąta
mając dane długości w treści zadania
i czy widzisz jakiś problem z taką wartością dla boku trójkąta
mając dane długości w treści zadania 
 bo musi być mniejsze od 9
bo musi być mniejsze od 9

 I co to by wtedy oznaczało
I co to by wtedy oznaczało 


 a dwa z nich nie są
spełnione nawet dla mocnego szacowania jakim jest a1 < 3
a dwa z nich nie są
spełnione nawet dla mocnego szacowania jakim jest a1 < 3
 1) α+γ=90o
2) Po dorysowaniu przystających trójkątów: ( niezbyt dokładny rysunek)
|∡YAX|=90o
ΔYAX− Δprostokątny równoramienny .
|XY|=3√2
3)
W ΔCXY:
25=18+16−2*3√2*4cosδ
1) α+γ=90o
2) Po dorysowaniu przystających trójkątów: ( niezbyt dokładny rysunek)
|∡YAX|=90o
ΔYAX− Δprostokątny równoramienny .
|XY|=3√2
3)
W ΔCXY:
25=18+16−2*3√2*4cosδ
 II sposób :
α+γ=90o
1) W ΔXAB:
II sposób :
α+γ=90o
1) W ΔXAB: