równoległobok orbit: Niech ABCD będzie równoległobokiem z BC=5, a M będzie takim punktem na boku CD, że MC:MD=4:3. Załóżmy, że BM,AM są prostopadłe odpowiednio do AC,BD. Oblicz pole ABCD.

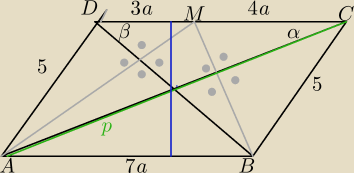
a7: P_ABCD=35a P_ABCD=1/2p*q*sin(α+β) 25=(7a)²+p²−2*7apcosα 25=(7a)²+q²−2*7aqcosβ _________________________ 0=p²−q²−14apcosα+14aqcosβ

	H2		H		H2		H
cosα=		=		cosβ=		=
	2p		p		2q		q

	H		H
0=p2−q2−14ap		+14aq
	p		q

p²=q² p=q jest to więc prostokąt (?)

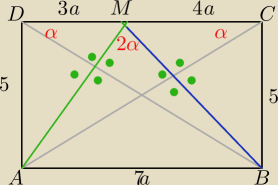a7: AM=√25+9a² BM=√25+16a² z tw. cosinusów dla ABM 49a²=25+9a²+25+16a²−2*√25+9a²√25+16a²cos2α

	49a2
cos2α=1−sin2α=1−2
	√25+49a2

https://www.wolframalpha.com/input/?i=24a%5E2-50%3D2%28%2825%2B9a%5E2%29%2825%2B16a%5E2%29%29%5E%281%2F2%29*%281-2*%28%2849a%5E2%29%2F%2825%2B49a%5E2%29%29 a=5√3{73}

	3
PABCD=35a=205√
	73

a7: ?

a7: niestety pomyliłam cosinusy z sinusami...

www: Czy ktoś obliczył mi wyszło 105√7/8