Sposoby rozwiązywania nierówności Ola: Mam dość nietypowe pytanie. Zastanawiam się, dlaczego sposób pierwszy rozwiązywania nierówności jest uznawany za prostszy niż drugi sposób rozwiązywania takich nierówności? Pierwszy sposób:

2
	>2 |x2
x

2x>2x² x−x²>0 x(1−x)>0 x>0 1−x>0 x<0 1−x<0 −x>−1 −x<−1 x<1 x>1 x∊(0,1) x∊∅ x∊(0,1) Drugi sposób:

2		2
	>2 | x>0		>2 | x<0
x		x

2>2x 2<2x 1>x 1<x x<1 x>1 x∊(0,1) x∊∅ x∊(0,1) Osobiście uważam, że drugi sposób jest krótszy i nie rozumiem dlaczego pierwszy sposób należy do łatwiejszych. Z góry bardzo dziękuję

chichi: Pierwszy sposób nie wymaga takiego rozbicia jakie robisz.. Jeden Rabin powie tak, drugi nie

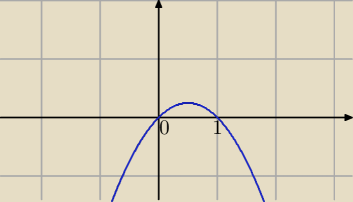
Mila: x(1−x)>0 korzystając z własności funkcji kwadratowej mamy odpowiedź: (patrz wykres) x∊(0,1)

Ola: Bardzo Państwu dziękuję Korzystając z własności funkcji kwadratowej nie ulega wątpliwości, że lepiej jest zastosować pierwszy sposób.

Szkolniak: Ja w 1 sposobie w momencie x(1−x)>0 nie rozpisywałbym tego na (x>0 i 1−x>0) v (x<0 i 1−x<0), tylko x(1−x)>0 ⇔ −x(x−1)>0 ⇔ x(x−1)<0 Ja np. w takich nierównościach byłem uczony, że przerzucamy wszystko z prawej strony na lewą, sprowadzamy do wspólnego ułamka i 'zamieniamy' iloraz na iloczyn.

wredulus_pospolitus: Ponieważ w pierwszym sposobie uczniowie muszą się o wiele bardziej 'postarać' aby popełnić błąd (głównie chodzi o znak nierówności, ale także zapisanie ostatecznego wyniku w przypadku gdy oba przypadki dają jakieś cząstkowe przedziały.

ICSP: Problem pojawi się jeśli w mianowniku wystąpi jakiś bardziej złożony wielomian. Dla przykładu:

1
	> 1
(x−1)(x−2)(x−3)(x−4)

Nadal będą tylko 2 przypadki ale ogólne przedziały na jakich będziesz operować znacznie się skomplikują. Już nawet nie wspominając o tym, że na koniec bierzesz iloczyn rozwiązań z uwzględnieniem tych przedziałów. Wtedy łatwo o pomyłkę. Osobiście polecam metodę z przerzucaniem wszystkiego na jedną stronę, następnie sprowadzaniem do wspólnego mianownika i na koniec zamianą ilorazu na iloczyn.

chichi: @Szkolniak ta 'zamiana' ilorazu na iloczyn powstaje właśnie w ten sposób jaki przedstawiał @Ola przemnożenie obu stron przez mianownik do kwadratu Tylko to rozbicie na przypadki nierówności kwadratowej jest zbędne.

Ola: Jeszcze raz bardzo dziękuję

Ola: @chichi sądzę, że te rozbicie na przypadki jest konieczne, gdy nie zostały wcześniej poznane własności funkcji kwadratowej.

wredulus_pospolitus: @Ola ... o jakich własnościach funkcji kwadratowej mówisz Metodę wężyka miałaś https://matematykaszkolna.pl/strona/142.html Jeżeli tak − to masz wszystko co potrzebne do rozwiązania tego typu nierówności bez rozbijania na jakiekolwiek przypadki

Szkolniak: @chichi wiem wiem, mówię tylko jakim schematem byłem uczony w szkole i z tego co pamiętam na tamte czasy całkiem sprawnie to szło także postanowiłem że napiszę, może Ola skorzysta i sama stwierdzi jak lepiej

Ola: @wreduluspospolitus W podręczniku do klasy pierwszej liceum Oficyna Edukacyjna Krzysztof Pazdro, w pierwszym dziale niestety są same nierówności bez znajomości funkcji kwadratowej ( ta jest w dziale czwartym wspomnianego podręcznika). Stąd wynikało moje rozbicie nierówności na przypadki.

Ola: @Szkolniak również dziękuję

wredulus_pospolitus: Olu ... w podstawówce nie miałaś metody wężyka? Serio aż tak podupada system edukacji ? Ecccchhhhhh

wredulus_pospolitus: To w takim razie − polecam Ci się zapoznać z tą metodą, zapamiętać ją ... bo nieraz będziesz jej używała w późniejszym czasie

Ola: Z tego co się orientuję, to nierówność wielomianowa już odkąd powstało gimnazjum została przeniesiona do szkół ponadpodstawowych. Proszę zerknąć do podstawy programowej, może coś mi umknęło

chichi: Przepraszam, ale orientujesz się w takich bzdetach, a w praktycznych rzeczach już nie? P. S. Czy podstawa programowa, to jest SUFIT?

Karolina: Ja tylko tłumaczę skąd moje rozumowanie. Chciałam użyć sposobu znanego większości uczniom klas pierwszych szkół ponadpodstawowych. Czy to jest jakaś zbrodnia matematyczna?

chichi: A to ja nie wiem kto uczy takimi metodami.. Nevermind P. S. Zapomniałaś zmienić nicku

Karolina: Przepraszam za zmianę imion (posiadam dwa imiona), a czasami piszę z telefonu, a czasami z komputera stąd ta zmiana (wyjaśniam z góry).