15 lip 16:23
ite: wskazówki pozwalające rozwiązać samodzielnie
z konstrukcji wynika, że OF i EO są promieniami, więc
|OF|=|OE|=|OC|
stąd wynika że
OF⊥ OC
oraz ΔFOC jest prostokątny równoramienny
a ΔEFO równoramienny
ΔAEF również jest równoramienny
pokaż że ΔEFO ≡ ΔAEF cecha kbk
15 lip 17:18
Natka: Czemu OF jest prostopadły do OC
15 lip 17:38
Minato:
ΔOCF jest równoramienny oraz <OCF = 45 i <OFC = 45, zatem <FOC = 90
15 lip 17:46
Natka: skad to <OCF = 45 i <OFC = 45

15 lip 21:28
chichi:
Bez jaj.
15 lip 21:31
chichi:
Czym jest czworokąt ABCD? Na jakie trójkąty dzielą przekątne tenże czworokąt?
15 lip 21:33
Natka: Ok już wiem jak zrobić to zdanie
15 lip 21:44
Alabb:
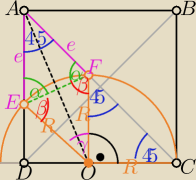
α+β=135
o to γ=45
o
więc czworokąt AEOF jest rombem
co daje tezę : |OF|=|OE|=|AF|=|AE|
15 lip 23:06
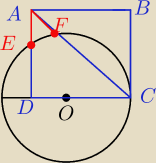 Dany kwadrat ABCD i półokrąg o środka O. Wiedząc że AE=AF pokaż, że promień=OF=FA.
Tu rysunek: https://nfhost.me/image/rys.aYPAh
Dany kwadrat ABCD i półokrąg o środka O. Wiedząc że AE=AF pokaż, że promień=OF=FA.
Tu rysunek: https://nfhost.me/image/rys.aYPAh

 α+β=135o to γ=45o
więc czworokąt AEOF jest rombem
co daje tezę : |OF|=|OE|=|AF|=|AE|
α+β=135o to γ=45o
więc czworokąt AEOF jest rombem
co daje tezę : |OF|=|OE|=|AF|=|AE|