okrągły stół HGH: na ile sposobow mozna rozsadzic 10 osob przy okraglym stole tak aby trojka osob siedziała obok siebie, i dwie pary? Zrobiłem tak rozstawienie trójki − 3! dwójki 2! dwójki 2! i teraz traktując trójki i dwójki jako osoby mam, 6 osób więc mogę je rozstawić na 6!/6 sposobów co finalnie daje mi 3!*2!*2!*5! sposobów jest ok?

wredulus_pospolitus: moim zdaniem powinno być 3krotnie mniej czyli: 2³*5!

HGH: Dlaczego? Co jest złego w moim rozwiązaniu w takim razie?

kerajs:

6!3!2!2!
10

Moim zdaniem wynik należy podzielić przez 10 ze względu na okrągły stół (i w domniemaniu nierozróżnialne miejsca przy nim).).

daras: https://matematyka.pl/viewtopic.php?t=372375

HGH: kerajs, dlaczego przez 10? skoro 'połaczyliśmy' tą trójke i dwie dwójki to nie powinniśmy dzielić przez 6?

wredulus_pospolitus: HGH ... załóżmy, że mamy tylko trójkę która ma siadać obok siebie. Wedle tego co napisałeś mamy:

	8!
3!*		= 3!*7!
	8

A zróbmy 'na raty': 1) siada pierwszy z trójki − 1 sposób 2) siada drugi z trójki − 2 sposoby 3) siada trzeci z trójki − 2 sposoby 4) siadają pozostali − 7! sposobów w efekcie mamy: 4*7! sposobów Dwa różne podejścia ... dwa różne wyniki ... który z nich jest błędny?

kerajs: Dzielę przez 10, gdyż mimo ''łączenia'' osoby zajmują 10, a nie 6 krzeseł.

HGH: wredulus − no rzeczywiście sposobem 'na raty' też wydaję się być dobrze. No to jak w końcu? kerajs − ale własnie rozmieszczając ich w obrębie 3 na 3! i dwójek na 2! już się tym nie zajeliśmy?

wredulus_pospolitus: dobra ... to co ja napisałem jest błędnie (to działanie 'na raty') bo nie obejmuje możliwości: 132 oraz 231

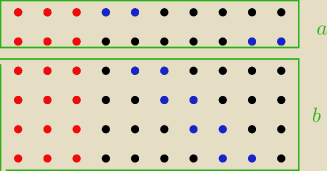
wredulus_pospolitus: tak więc ... Twój oryginalny wynik powinien być poprawny. Zróbmy 'poprawione na raty' dla sprawdzenia: 1) ustawiamy trójkę − 3! sposobów 2) siadają − 1 sposób 3) ustawiamy pierwszą parę (kto po lewej siedzi) − 2 sposobów 4a) para siada bezpośrednio przy trójce − 2 sposoby 5a) wybieramy kolejność drugiej pary − 2 sposoby 6a) siada 'lewy' z tej pary na jednym z 4 krzeseł nie może mieć po prawej zajętego) − 4 sposoby 7a) drugi siada obok − 1 sposób 8a) reszta siada − 3! 3!*1*2³*4! 4b) para nie siada bezpośrednio przy trójce (czyli 'lewy' ma do wyboru 3 krzesła) − 4 sposoby 5b) − 2 sposoby (wybór lewego z drugiej pary) 6b) siada lewy − nie może usiąść tam gdzie po prawej ma zajęte (2 takie krzesła) − 3 sposoby 7b) siada prawy − 1 sposób 8b) siada reszta − 3! sposobów 3!*1*2*4*2*3*3! = 3!*2²*3*4! 3!*1*2³*4! + 3!*3²*4! = 3!*4!*(8 + 12) = 3!*2*5*4! = 3!*2!*5! 3 Rysunek przedstawia rozłożenie trójki i pierwszej pary dla obu przypadków

wredulus_pospolitus: a końcu miało być bez tej '3' po 5!

HGH: