podzielne liczby HGH: wsord liczb 1,2...800 ile jest liczb które nie są podzielne przez 7, ale są podzielne przez 6 lub 8. Zacząłem tak: Podzielne porzez 7 = 114 więc niepodzielnych = 686 Podzielne przez 6 = 133 podzielne przez 8 = 100 podzielne przez 6 i 8 = 33 więc podzielne przez 5 lub 8 = 133+100−33 = 200 Co dalej? czy to wogóle dobra droga? bo chyba się zgubiłem...

wredulus_pospolitus: źle zacząłeś

wredulus_pospolitus: chcesz policzyć: liczby podzielne przez 6 + liczby podzielne przez 8 − liczby podzielne przez 6,8 − liczby podzielne przez 6,7 − liczby podzielne przez 8,7 + liczby podzielne przez 6,7,8 dlaczego tak ... otóż: 1) pierwsze trzy człony dają Ci ile jest liczb podzielnych przez 6 LUB 8 2) dorzucając dwie kolejne odejmujesz te które są podzielne przez 6 i 7 lub 6 i 8 3) ale później musisz dorzucić (bo dwukrotnie odjąłeś) ile jest liczb podzielnych przez 6 i 7 i 8

HGH: Właśnie w trakcie tak pomyślałem, to jak zacząć? Tutaj mam problemem z tym warunkiem podzielności przez 7...

HGH: nadal nie rozumiem, tych członów już zwłaszcza

wredulus_pospolitus: nie rozumiem co ma warunek podzielności przez 7 tutaj? najmniejsza podzielna przez 7 to a₁ = 7 a_n = 7n ≤ 800 −−−> szukasz największego 'n' spełniającego tę nierówność

HGH: podzielnych przez 7 to już mam, wyszło mi ich 114. Ale gubię się w tym które mam odjąć a które dodawać do siebie

wredulus_pospolitus: 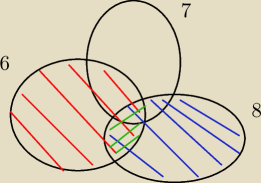podzielne przez 6 podzielne przez 8 podzielne przez 6 i 8

HGH: aaa okej, z rysunkiem już chyba dam radę

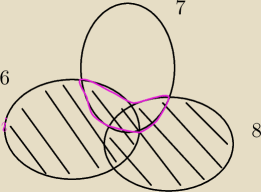
wredulus_pospolitus: w efekcie dostaje (po tych dodaniu dwóch pierwszy i odjęciu trzeciego czarny obszar) i musisz się jeszcze 'pozbyć' fioletowego obszaru