kombinatoryka
Jarel:
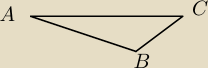
Na ile sposobów można dodać kolejny trójkąt do trójkąta ABC na rysunku, aby się nie nakładały i
razem tworzyły trójkąt równoramienny?
10 lip 12:30
wredulus_pospolitus:
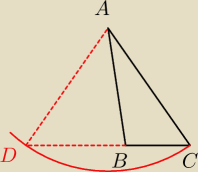
inaczej ułożę ten trójkąt
po dołożeniu trójkąta ABD otrzymujemy ACD który jest równoramienny.
10 lip 13:27
wredulus_pospolitus:
czekaj czekaj ... to zadanie jest z działu kombinatoryka
10 lip 13:28
Jarel: Czyli tylko 1 sposób
10 lip 14:38
wredulus_pospolitus:
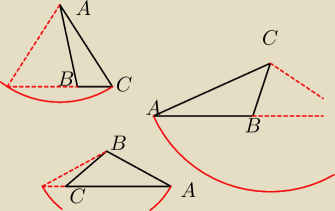
nie ... potencjalnie trzy takie trójkąty można zrobić
10 lip 15:14
wredulus_pospolitus:
10 lip 15:40
kerajs:
5
10 lip 16:31
Jarel: A jakie jeszcze dwa?
10 lip 21:07
wredulus_pospolitus:
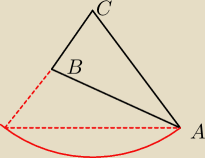
Jarel np tak można.
Czym się różni od poprzednich ... tym, że teraz podstawa to bok z dopisywanego trójkąta (a nie
jak wcześniej jedno z ramion).
10 lip 22:49
wredulus_pospolitus:
nie do końca się zgodzę z tym co kerajs napisał ... jeżeli wyjściowy trójkąt nie można 'odbić'
(czyli z trójkąta ABC zrobić trójkąt ACB) oraz jest rozwartokątny (lub prostokątny) to mamy:
3 możliwości dopisania tak, że bok z wyjściowego trójkąta jest częścią podstawy trójkąta
równoramiennego (częścią podstawy jest AB, AC, BC)
2 możliwości dopisania tak, że jeden bok trójkąta ABC jest ramieniem, drugi częścią jego
ramienia (patrz rysunek z 22:49) −−− jeżeli kąt rozwarty jest przy wierzchołku B, to tenże
wierzchołek nie może być w pozycji wierzchołka A z rysunku o 22:49.
To w sumie daje nam 5 możliwości i pokrywa się z tym co napisał kerajs.
Jeżeli jednak wyjściowy trójkąt ABC jest ostrokątny (i nadal nie można go odbić), to mamy w
sumie 6 możliwości (bo dochodzi sytuacja gdy wierzchołek B jest na pozycji wierzchołka A z
rysunku 22:49).
Tak więc −−− wszystko zależy od tego jaka jest miara największego kąta w trójkącie ABC.
10 lip 23:45
11 lip 06:34
kerajs:
''Tak więc −−− wszystko zależy od tego jaka jest miara największego kąta w trójkącie ABC.''
A co z sytuacją: B rozwarty, C=600 ?
11 lip 09:24
wredulus_pospolitus:
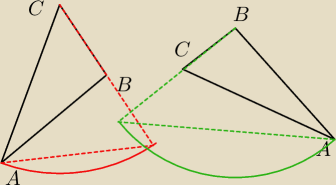
kerajs ... jeżeli B jest rozwarty to mamy takie dwie sytuacje (pomijam trzy pierwotnie
pokazane).
W obu tych przypadkach ramieniem będzie bok AB, stąd też kąt przy wierzchołku C (równy 60
o) ma
zerowe znaczenie.
Wiemy, że kąt A < kąt C < kąt B (zależności długości przeciwległych boków) związku z tym:
2*(∡A) + ∡B < 180
o <−−− obie zaprezentowane sytuacje zawsze będziemy mogli wykonać
i jedynie odpada sytuacja z ∡B przy podstawie ze względu :
∡A + 2*(∡B) > 180
o
11 lip 12:32
wredulus_pospolitus:
cholera ... faktycznie zawsze będzie 5 możliwości .. bo zawsze w zaprezentowanym trójkącie ABC
mamy:
∡A + 2*(∡B) > ∡A + ∡B + ∡C = 180
o 
mea kulpa
11 lip 12:37
kerajs:
Hmm... , w końcu narysowałem sobie trójkącik z pierwszego postu i ... wychodzi mi 6 (szlag!)
możliwych trójkątów.
W sytuacji gdy C=60o jest ich tylko 5.
Przepraszam za wprowadzenie w błąd. Mea maxima culpa.
11 lip 14:15
wredulus_pospolitus:
jak 6 możliwości
wierzchołek B nie może być przy podstawie (gdy podstawa to bok dorysowanego trójkąta)
bo 2∡B + ∡A > ∡C + ∡B + ∡A = 180
o, a kąt przy podstawie będzie większy równy od ∡B.
To jakie 6 możliwości masz? Możesz je naszkicować?
11 lip 14:22
11 lip 14:56
