całka oznaczona
wakacje: witam mam pytanie odnośnie całki oznaczonej z wartością bezwzględna
mam taki przykład: −1010∫|x2−5x+6|dx
czy to będzie po prostu −102∫(x2−5x+6)dx+23∫(−x2+5x−6)dx+310∫(x2−5x+6)dx?
8 lip 21:24
wakacje: końcowo wyszło mi że całka ta równa jest −100
8 lip 21:30
Maciess: Nie wiem jak rachunki, no ale generalnie tak.
8 lip 21:42
ICSP: Liczysz całkę z funkcji która przyjmuje tylko wartości dodatnie i w wyniku otrzymujesz liczbę
ujemną?
Znasz interpretację geometryczną całki?
8 lip 21:51
wredulus_pospolitus:
Skoro funkcja podcałkowa jest z wartością bezwzględną to jakim cudem może wynikiem całki być
ujemna wartość?
Ujemna wartość całki oznaczonej oznacza, że większość pola pomiędzy krzywą a osią OX jest
poniżej osi OX (czyli funkcja musi przyjmować wartości mniejsze od 0, co jest niemożliwe w
przypadku funkcji z nałożoną wartością bezwzględną

)
8 lip 21:52
chichi:
−10 ∫
10|x
2−5x+6|dx=
=
−10 ∫
2(x
2−5x+6)dx −
2 ∫
3(x
2−5x+6)dx +
3 ∫
10(x
2−5x+6)dx =
| | x3 | | 5 | | x3 | | 5 | |
= [ |
| − |
| x2+6x]−102 − [ |
| − |
| x2+6x]23 + |
| | 3 | | 2 | | 3 | | 2 | |
| | x3 | | 5 | | 1 | | 833 | |
+ [ |
| − |
| x2+6x]310 = 648 + |
| + |
| = 787 |
| | 3 | | 2 | | 6 | | 6 | |
8 lip 22:44
Mila:
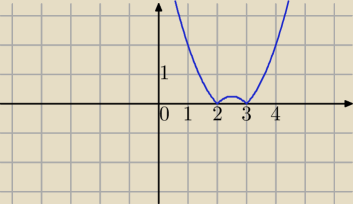
x
2−5x+6=0⇔x=2 lub x=3
|x
2−5x+6|=x
2−5x+6 dla x≤2 lub x≥3
|x
2−5x+6|=−x
2+5x−6 dla x∊(2,3)
wynik: 787
8 lip 22:50
wakacje: głupi błąd, nie wiem co ja zrobiłem i przez to wyszła jakaś głupota, przepraszam i dziękuję za
rozwiązania
9 lip 01:08
 )
)
 x2−5x+6=0⇔x=2 lub x=3
|x2−5x+6|=x2−5x+6 dla x≤2 lub x≥3
|x2−5x+6|=−x2+5x−6 dla x∊(2,3)
wynik: 787
x2−5x+6=0⇔x=2 lub x=3
|x2−5x+6|=x2−5x+6 dla x≤2 lub x≥3
|x2−5x+6|=−x2+5x−6 dla x∊(2,3)
wynik: 787