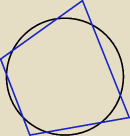
okrąg gooq: Okrąg i czworokąt ułożone są tak, jak pokazano na rysunku. Sumy długości przeciwległych łuków okręgu leżących wewnątrz czworokąta są równe. Udowodnij, że na tym czworokącie da się opisać okrąg.

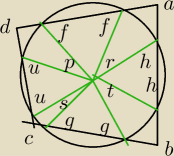jc: Litery oznaczają kąty (a,b,c,d powinny być wewnątrz, ale nie było miejsca). a+c = 360 − (180−f) − (180−h) − r + 360 − (180−g) − (180−u) − s = f+h+g+u− r−s b+d = f+g+h+u − p−t ale z założenia r+s=p+t. Dlatego a+c = b+d, co oznacza, że czworokąt można wpisać w okrąg.