funkcja wykladnicza Hashiri: Rozwiaz nierownosc: 3^x≤5*5^x+3

	3
mam wyjsc x≥log		625
	5

ale cos nie moge do tego doprowadzic staje na tym, ze x≥log₅3^x−4 Pomocy

Hashiri: Przepraszam ze blad w pisaniu w odpowiedziach jest wynik x≥log_³5625

Godzio: 3^x ≤ 5 * 5^x * 125 3^x ≤ 625*5^x /: 5^x

	3
(		)x ≤ 625
	5

x≤log_3/5625

Hashiri: Dzieki

Eta: Godzio x ≥ log_3/5 625 bo przy oodstawie a€(0,1) ... następuje zmiana zwrotu nierówności , bo funkcja jest malejąca

Hashiri: a tak Eta ma racje zly znak dales

Eta:

Godzio: no tak przeoczyłem

Hashiri: Mam jeszcze taki dylemat Jak mam np log_0,5x>log_0,52 to x<2 a jak mam np. : log_0,5x>−1 to x > 2 czy x < 2 Nie wiem w ktora strone dac znak

Hashiri: Pomoze ktos

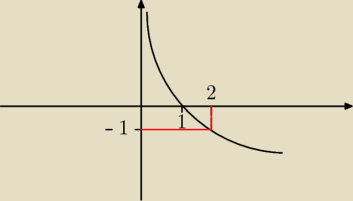
Godzio: po wykresie, teraz widać kiedy log_0,5x > −1 ?

Hashiri: a no tak, poza tym zamiast 1 mozna tez wstawic logarytm o podstawie 0,5 Dzieki

Hashiri: Jeszcze nie wiem jak rozwiazac : log_x4<1

Hashiri: Zrobilby mi ktos P.S. Przepraszam ze jestem taki niecierpliwy

Eta: rozpatrujesz w dwu przypadkach: dla podstawy logarytmu: 1) dla x€ ( 0,1) otrzymujesz zminę zwrotu nierówności ( bo f. malejąca) x¹ >4 => x >4 i x€( 0,4) −−− sprzeczność 2) dla x >1 ,.... nie ma zmiany zwrotu nerównosci x¹ <4 i x >1 => x€( 1, 4) rozwiazązaniem tej nierównosci jest x€ ( 1, 4)

Hashiri: 1 wiem, ze dla x∊(0,1) jest zmiana zwrotu czyli chyba powinno byc x<4 i x∊(0,1) to x∊(0,1) 2 przypadek to wiem i rozumiem )

Basia: log_x4<1 ⇒ dla x∊(0,1) x¹>4 tu jest zmiana zwrotu i oczywiście sprzeczność

Hashiri: Mi wychodzi jakos tak : log_x4<1 dla x∊(0,1) log_x4<log_xx (zmieniam znak) 4>x i wychodzi ze x∊(0,1) Nie wiem co robie zle

Basia: niedobrze; jeśli tak to log_x4<log₄4 x>4 podstawy tu porównujesz, a nie liczby logarytmowane

Hashiri: moze masz i racje, ale mam w odpowiedziach ze x∊(0,1)∪(4,∞) wiem tez ze czesto w odpowiedziach sa bledy ale jak korzystam z roznowartosciowosci funkcji to biore pod uwage 'x' i 'y', a nie raczej podstawe 'a', przynajmniej jeszcze nigdzie o tym nie przyczytalem

Basia: To prawda. dla x∊(0,1) log_x4<0 jest więc też <1 aby logarytm był >0 i <1 podstawa musi być większa od liczby logarytmowanej czyli x>4 czyli x∊(4;+∞) co w sumie daje Twoją odpowiedź

Basia: Nie przeczytałam wczesniej porządnie o co chodzi.

Basia: Tak tylko to wszystko o czym była mowa wyżej dotyczy funkcji y=log_ax A Ty masz funkcję y=f(x) = log_x4 to zupełnie inna funkcja w (0,1) rosnąca; natomiast w (1;+∞) malejąca