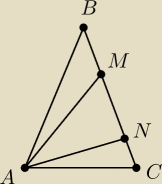
 Punkty M i N leżą na ramieniu BC trójkąta równoramiennego ABC tak ze MN=AN. Wiedząc ze kąt BAM=
kąt NAC, oblicz kąt MAC.
Punkty M i N leżą na ramieniu BC trójkąta równoramiennego ABC tak ze MN=AN. Wiedząc ze kąt BAM=
kąt NAC, oblicz kąt MAC.
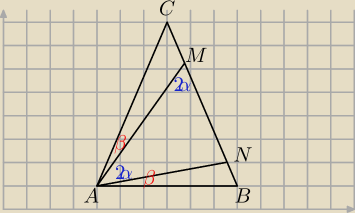 <ABC = 2α+2β
<ACB = 180−(4α+4β)
w ΔAMC
<ACM = 180−(180−2α+β)=2α−β
180−4α−4β=2α−β
180 = 6α+3β
2α+β=60
=======
<ABC = 2α+2β
<ACB = 180−(4α+4β)
w ΔAMC
<ACM = 180−(180−2α+β)=2α−β
180−4α−4β=2α−β
180 = 6α+3β
2α+β=60
=======
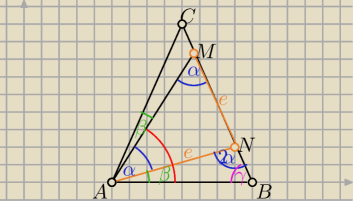 2β+α=γ i β+2α+γ=180o
to 3β+3α=180o ⇒ α+β=60o = |∡MAN|
2β+α=γ i β+2α+γ=180o
to 3β+3α=180o ⇒ α+β=60o = |∡MAN|