Proszę o rozwiązanie:
Agnieszka88: 1. Określić dziedzinę oraz zbadać ekstrema funkcji dwóch zmiennych
f(x,y) = − 13x3 + y3+x − 3y+ 13
2.Obliczyć całkę podwójną ∬D 𝑥𝑑𝑥𝑑𝑦 jeśli 𝐷 − obszar ograniczony krzywymi
𝑦=0, 𝑥−y =2 , 𝑥+𝑦 = −2
3. Obliczyć objętość bryły ograniczonej powierzchniami z = 3x, x2 + y2 =4, x = 0 , y = 0,
z =0
4. Obliczyć całkę krzywoliniową ∫k (𝑥+𝑦)𝑑𝑙 , gdzie krzywa K jest trójkątem o wierzchołkach
𝐴(−1,0), 𝐵(1,0), 𝐶(0,1).
5. Wyznaczyć pierwsze i drugie pochodne cząstkowe funkcji dwóch zmiennych 𝑧 = exy2 .
Wynik doprowadzić do najprostszej postaci.
28 cze 18:33
wredulus_pospolitus:
no ... fajne zadania ... i co z nimi?
dziedziny w pierwszym nie potrafisz określić
pochodnych cząstkowych w ostatnim nie potrafisz policzyć
28 cze 18:52
Agnieszka88: 1. D = R2 i trzeba policzyć 1 i 2 pochodne cząstkowe po x,y tyle wiem.
5. Tej pochodnej cząstkowej niestety nie umiem zrobić
28 cze 22:44
HGH: 5. jesli liczysz pochodna po 'x' to y traktujesz jako stałą, jeśli pochodną po 'y' to x jak o
stałą
28 cze 23:11
Mila:
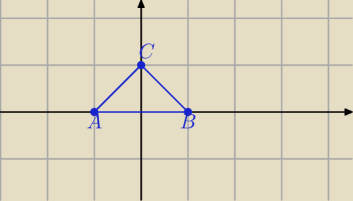
∫k (𝑥+𝑦)𝑑𝑙 , gdzie krzywa K jest trójkątem o wierzchołkach
𝐴(−1,0), 𝐵(1,0), 𝐶(0,1).
1) AC:
y=x+1, −1≤x≤0
x=t, y=t+1, −1≤t≤0
x'=1dt, y'=1 dt
dl=
√(12+12dt=
√2dt
Wzdłuż AC:
∫
AC (𝑥+𝑦)𝑑𝑙 =
−1∫
0(t+t+1}
√2dt=
√2−1∫
0(2t+1) dt=
√2[t
2+t]{−1}
0=
=
√2(0−(1−1))=0
2) Wzdłuż CB:
y=−x+1, x∊<0,1>
x=t, 0≤t≤1, y=−t+1
x'=1,y'=−1
dl=
√12+(−1)2dt=
√2dt
∫
AC (𝑥+𝑦)𝑑𝑙 =
0∫1(t−t+1)
√2dt=
√2[t ]
01=
√2(1−0)=
√2
3) Wzdłuż AB
x=t, −1≤t≤1, y=0
x'=1, y'=0
dl=
√1+0dt=1dt
| | 1 | |
∫AB(t+0)√2dt=−1∫1√2 t dt=√2 [ |
| t2]−11= |
| | 2 | |
4)
∫k (𝑥+𝑦)𝑑𝑙 =
√2
28 cze 23:28
janek191:
z.5
Niech z = f(x,y) = ex y2
f 'x(x,y) = e xy2*y2 = y2 ex y2
f 'y(x,y) = e x y2*2x = 2 x *ex y2
f ''xx(x,y) = y2*exy2*y2 = y4 ex y2
f ''xy(x,y) = 2y*exy2 + y2*exy2*2y = ...
itd.
29 cze 07:32
piotr:
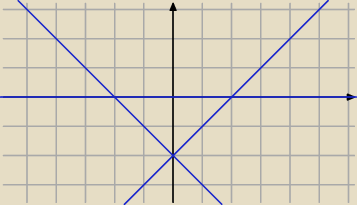
2.
∫
−20∫
−x−20x dy dx + ∫
02∫
x−20x dy dx =
∫
−20(x+2)x dx + ∫
02(−x+2)x dx =
(x
3/3+x
2|
−20 + (−x
3/3+x
2|
02=
2
3/3−2
2−2
3/3+2
2 = 0
29 cze 07:48
piotr: 3.
∫0π/2∫02 3r2cosφ dr dφ = r3|02 sinφ|0π/2 = 8
29 cze 08:00
Agnieszka88: Mila w 4 ∫AB (t+0)√2dt zamiast √2dt nie powinno być 1dt ?
29 cze 13:11
circle:
POwinno być: ∫
AB(t+0)dt.
29 cze 15:12
Damian#UDM: Zostawiam komentarz, ta wiedza bardzo się przyda
29 cze 15:35
Damian#UDM: Głównie mi chodzi o całkę krzywoliniową − to temat, który chce niedługo ogarnąć
29 cze 15:36
Mila:
Zadanie dla Agnieszki i Damiana.
Oblicz całkę krzywoliniową:
∫K(x+y)dl gdzie K jest obwodem Δ o wierzchołkach
A=(0,0), B=(1,0), C=(0,1)
29 cze 17:29