pochodna kierunkowa Damian#UDM: Narysować na płaszczyźnie zbiór punktów, w których pochodna kierunkowa funkcji f(x,y)=y√xarctg(x+y) w kierunku wersora v=(^−√2₂, ^√2₂) jest równa 0.

Adamm: trzeba wyznaczyć punkty (x₀, y₀) dla których

	df		df
(		(x0, y0),		(x0, y0))*v = 0
	dx		dx

Damian#UDM: Każda z tych współrzędnych ma się równać zero?

ICSP: Iloczyn skalarny ma się równać zero.

Damian#UDM: A, czyli wstawiam pochodne pierwszego rzędu w te nawiasy i mnożę razy wersor i rozwiązuje równanie?

ICSP: Zależy co rozumiesz poprzez stwierdzenie: "mnożę przez wersor" W dużym uroszczeniu tak.

Damian#UDM: że mnożę współrzędne x−owe ze sobą i dodaje pomnożone współrzędne y−owe i ma to równanie być równe 0. f'_x*v_x+f'_y*v_y=0

ICSP: czyli mnożysz skalarnie. Tak właściwie to równanie po podstawieniu zredukuje się do prostszego: f_x(x₀,y₀) = f_y(x₀,y₀)

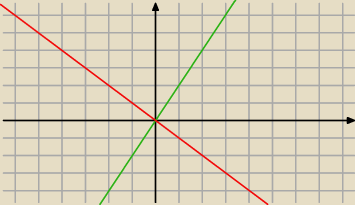
Damian#UDM: Dziedzina f i pochodnej po y : x≥0 i y∊R Dziedzina pochodnej po x : x>0 i y∊R Po mnożeniu skalarnym otrzymałem

	yarctg(x+y)
√xarctg(x+y)=		|*2√x
	2√x

2xarctg(x+y)=yarctg(x+y) yarctg(x+y)−2xarctg(x+y)=0 arctg(x+y)*[y−2x]=0 arctg(x+y)=0 lub y−2x=0 x+y=tg(0) lub y=2x y=−x lub y=2x Jest git? Co teraz trzeba zrobić?

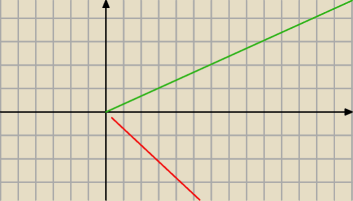
Damian#UDM: Z tego względu, że x>0

ICSP: Sprawdź pochodne cząstkowe.

Damian#UDM:

	yarctg(x+y)		y√x
f'x=		+
	2√x		(x+y)2+1

	y√x
f'y=√xarctg(x+y)+
	(x+y)2+1

ICSP: a faktycznie są poprawne. Przepraszam bardzo Rozwiązaniem są te dwie półproste które narysowałeś. Oczywiście bez punktu (0,0).

Damian#UDM: Ufff, już myślałem, że kartka zapisana do wyrzucenia