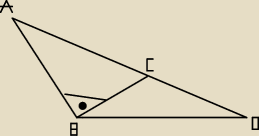
Wyznacz długość AC saubeer: Wyznacz długość boku AC jeżeli AB=CD=1cm oraz miary kątów ABC oraz CBD wynoszą następująco 90 oraz 30 stopni.

chichi: Jak wciśniesz literkę 'T' w panelu rysowania, to możesz wprowadzać tekst na rysunku

Pola: Oznacz AC=a wtedy z tw sinusów i Pitagorasa dojdziesz do a⁴+2a³−2a−4=(a³−2)(a+2)=0

Maja:

	√3
W ΔAEB : |AE|=
	2

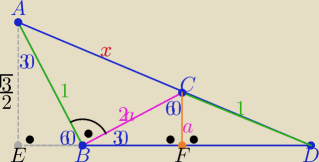
Z podobieństwa trójkątów AED i CFD z cechy (kkk)

√3		x+1		√3
	=		⇒ 2a=
2a		1		x+1

Z tw. Pitagorasa w ΔABC :

	3
x2=1+4a2 ⇒ x2= 1+
	(x+1)2

otrzymujemy: (x+1)²(x²−1)=3 ⇒ x⁴+2x²−2x−4=0 (x³−2)(x+2)=0 |AC|= x=³√2

chichi:

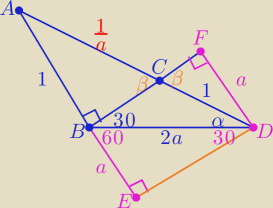
	a+1		1
(		)2=1+2a+4a2 ⇒		=3√2
	a		a

Maja: Rozwiń dokładniej to równanie...........

chichi: A co Ty @Eta już takich rzeczy nie robisz w pamięci, a może gryzie Cię, że krócej?

	a+1
(		)2=1+2a+4a2 ⇒ a2+2a+1=a2+2a3+4a4 ⇒ 4a4+2a3−2a−1=0 ⇒ (2a+1)(2a3−1)=0
	a

Maja: Jestem w jak się do mnie odnosisz ! Jakie krócej, jakie krócej ?

chichi: To w jakim celu miałem rozwijać to równanie? Pokazałem jasno skąd to wynika i myślę, że to nie rozwiązanie równania jest problemem autora. Kwintesencja rozwiązania jest na rysunku