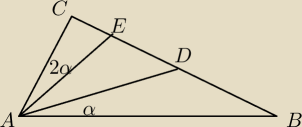
geometria friedric G.: Wiedzac, ze AC=BD, CE=2, ED=1, AE=4 oraz ∠CAE=2∠DAB. Wyznacz pole trojkata ABC.

chichi: Zadanie z jakiegoś konkursu?

friedric G.: chyba tak, niemniej jednak nie znalazlem jeszcze osoby, ktora by to zadanie rozwiazala. Ja niestety posiadam sam wynik od autora zadania, pozdrawiam

Mila: To podaj ten wynik

an:

	9
przy pomocy geogebry wychodzi mi		√15
	4

Mila: Dziękuję an. Jeśli się nie roztopię, to spróbuję poszukać pola

chichi: Potwierdzam wynik @an, bez użycia GeoGebry Poczekam na rozwiązanie od @Mila, moje jest nieco długie

wredulus_pospolitus: korzystając z tw. cosinusów dla kąta ∡ACB możemy wyznaczyć długość |AD| oraz jak zależy długość |AB| od |AC|=z później trzeba rozwiązać układ dwóch równań powstałe z tw. cosinusów dla ∡BAD i ∡EAC gdzie niewiadomymi będzie cosα oraz z = |AC| = |BD| mając boki trójkąta można wyznaczyć jego pole ale szczerze mówiąc ... patrząc na ten układ równań stwierdziłem, że nie chce mi się tego rozwiązywać

chichi: A jaka jest miara 'kąta ∡ACB'?

wredulus_pospolitus: nieistotne ... redukuje Ci się przy odejmowaniu równań .... dobra ... teraz zobaczyłem że źle podstawiałem do kolejnych równań tw. cosinusa

wredulus_pospolitus: chociaż nadal można tak zrobić ... wystarczy przemnożyć odpowiednio jedno równań przed odejmowaniem ich w celu likwidacji czynnika z cos(∡ACB)' Innymi słowy ... |AD| i |AB| uzależniamy od |AC| = z (nie są to śliczne zależności)

chichi: Nie mam teraz jak sobie tego rozpisać, a na sucho mi się nie chce myślę, zerknę jak wrócę, a jak Ci się chce, to wklep tu swoje rozwiązanie, ja później wrzucę swoje

a7: no i jak? czy ktoś rozwiąże to zadanie, bo mnie ciekawi, jak je zrobić?

wredulus_pospolitus: Oznaczenia: |AC| = |BD| = z |AD| = y |AB| = x z tw. cosinusów dla kąta ∡ACB 1) trójkąt ACE: 16 = z² + 4 − 4z*cosβ 2) trójkąt ACD: y² = z² + 9 − 6z*cosβ 3) trójkąt ACB: x² = z² + (3+z)² − 2z(3+z)*cosβ (1) i (2) 16 = z² + 4 − 4z*cosβ //*3 y² = z² + 9 − 6z*cosβ //*2 48 = 3z² + 12 − 12z*cosβ //*3 2y² = 2z² + 18 − 12z*cosβ //*2 odejmujemy: 2y² − 48 = −z² + 6 −−−> y² = 27 + z²/2 (1) i (3) 16 = z² + 4 − 4z*cosβ //*(3+z) x² = z² + (3+z)² − 2z(3+z)*cosβ //*2 48 + 16z = 3z² + z³ + 12 + 4z − 4z(3+z)cosβ 2x² = 2z² + 18 + 12z + 2z² − 4z(3+z)*cosβ

	z3+z2
odejmujemy: 2x2 − 48 − 16z = z3 + z2 + 8z + 6 −−> x2 =		+ 12z + 27
	2

z tw. cosinusów dla kątów α i 2α: 4 = 16 + z² − 8zcos(2α) = 16 + z² − 16zcos²α + 16z

	z3
z2 = y2 + x2 − 2xy*cosα =		+ z2 + 12z + 54 − 2√...*√...cosα
	2

układ równań z dwoma niewiadomymi (z i cosα) ... więc można to rozwiązać, mając z mamy x ... mamy wszystkie boki ... to mamy pole czy to optymalne rozwiązanie ... zapewne nie

a7: optymalne czy nie optymalne, ale chyba z grubsza rozumiem, dzięki

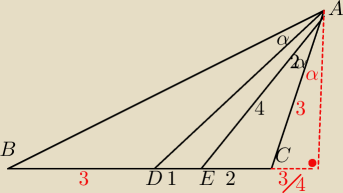
an: Tak to wygląda, ale jak uzasadnić te czerwone

chichi: @Mila gratuluję, jesteś jedyną osobą, która użyła w tym zadaniu tego twierdzenia. Ja zbieram się do wstawienia swojego rozwiązania, ale mi się po prostu nie chce, ale przedstawię plan, bo korzystałem z twierdzenia, którego nazwy użyłaś: (1) Twierdzenie o dwusiecznej (2) 2x twierdzenie Stewarta (nie Stewarda) (3) Twierdzenie Steinera I po zadaniu

Mila: Przedstaw plan

Mila: Tw.Stewarta można ominąć wykorzystując tw. cosinusów, ale jest więcej pisania. Trzeci punkt u mnie zbyteczny ( pomijam, że jest tam literówka). Niestety to nie jest koniec. Muszę jeszcze pomyśleć

Mila: chichi Wpiszę na nowo , bo nie wszystko tam było dobrze. Nie denerwuj się , że usunęłam wpis. Mam inny plan.

chichi: Mój plan z 00:37 szybko dosyć prowadzi do rozwiązania, próbowałaś?

Mila: Nie , zostawiam to dla Ciebie, bo to Twój pomysł

Mila: Dzisiaj oglądałam mecze

chichi: Ja to zrobiłem już w dzień publikacji zadania

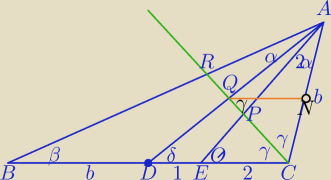
Mila: 1) Półprosta CR Dwusieczna kąta BCA Z tw . o dwusiecznej kąta

AR		b
	=
RB		b+3

2) Tw. Menelausa

AR		BC		DQ
	*		*		=1
RB		BD		QA

b		b+3		DQ
	*		}*		=1⇔
b+3		b		QA

|DQ|=|QA|⇒ Q jest środkiem AD W ΔCQN :

3		b
	=
2		2

b=3 Dalej juz proste.

Kacper: