Ktoś wie jak zrobić te zadania i nakieruje mnie. Treść zadań w linku. Kasia4391: Witam, ostatnio miałam takie coś na kolokwium i nie wiedziałam jak to zrobić, , spróbuje ktoś naprowadzić jak wykonać te zadania: 2,3,4,5,6 ? Treść zadań w linku. https://naforum.zapodaj.net/4298ccfa080b.png.html

Mila: Co zrobiłaś na kolokwium?

on: Jasno pisze : "nie wiedziałam jak to zrobić"

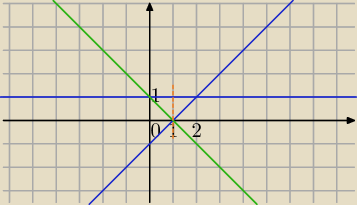
Mila: 2) Całka podwójna. ∫∫_D(2x)dxdy jeśli D − obszar ograniczony krzywymi y=1, x=y+1, x+y=1 x=−y+1 1) ₀∫¹[_x=−y+1∫^x=y+1(2x)dx]dy= =₀∫¹[x²]_−y+1^y+1]dy=₀∫¹[(y+1)²−(−y+1)²]dy= =₀∫¹(4y)dy=[2y²]₀¹=2 Albo zmieniasz kolejność całkowania i rozbijasz na dwie całki. ₀∫¹[_y=−x+1∫¹(2x)dy]dx+₁∫²[_y=x−1∫¹(2x)dy]dx= =₀∫¹({2xy]_−x+1¹)dx+₁∫²([2xy]_x−1¹)dx= =₀∫¹(2x²)dx+₁∫²(−2x²+4x)dx=

	2
=[U{2]{3}x3]01+[−		x3+2x2]12=
	3

	2		−16		2		14		2
=		+		+8−(−		+2)=−		+8+		−2=
	3		3		3		3		3

=2 Wybór należy do Ciebie

getin: 3) Objętość bryły P = ∫∫_D 2e^−x2−y2 dxdy, gdzie D − okrąg x²+y² = 4 Wprowadzamy współrzędne biegunowe x = r*cosφ y = r*sinφ J = r Obszar D zamieniamy w obszar Δ we współrzędnych biegunowych Δ: 0≤r≤2, 0≤φ≤2π ∫∫_D 2e^−x2−y2 dxdy = ∫∫_Δ 2e^−r2*r drdφ = = ∫₀^2π dφ ∫₀² 2r*e^−r2 dr = ... ∫₀² 2r*e^−r2 dr = |r² = t, 2rdr = dt| = = ∫₀⁴ e^−t dt = −e^−t |⁴₀ = −e⁻⁴ + e⁰ = 1−e⁻⁴ ... = ∫₀^2π 1−e⁻⁴ dφ = φ − e⁻⁴φ |^2π₀ = 2π − 2π*e⁻⁴ − 0 + e⁻⁴*0 = = 2π − 2π*e⁻⁴

Mila: 4) Podpowiedź: Uporządkuj dane rosnąco, oblicz średnią arytmetyczną skorzystaj z wzorów, aby obliczyć pozostałe wartości. ( na pewno masz w notatkach) Jeśli będą trudności to pisz.

circle:

daras: a kasia już dawno odleciała i nie wróci

circle: Wróciła dzisiaj , aby zapytać o następne zadania z kolokwium. Nie reaguje na rozwiązane

Damian#UDM: No 4. zadanie ciekawe jak resztę rzeczy policzyć

Kasia4391: Dziękuje za pomoc.

Mila: f(x,y)=cos(xy) 1) f_x=−sin(xy)*y=−y sin(xy) ( y traktujesz jak stałą ) f_xx=−y*( cos(xy)*y)=−y² cos(xy) f_xy=(−y sin(xy) )'=(−y)'*sin(xy)+(−y)*(sin(xy)'= ( x traktujesz jak stałą ) =−1sin(xy)−y*x cos(xy)= =−sin(xy)−xy cos(xy) 2) f_y=−x*sin(xy) ( x traktujesz jak stałą ) f_yy=−x *(cos(xy)*x=−x²cos(xy) f_yx=(−x*sin(xy) )'= (−x)'*sin(xy)+(−x)*(sin(xy))'=−sin(xy)−xy sin(xy) ( y traktujesz jak stałą )