Działania na kwantyfikatorach Kaczor: Udowodnij, że ∀(A∪B)^C=A^C ∩ B^C Nie mam pomysłu jak to udowodnić.

Kaczor: Ma ktoś jakieś propozycje?

chichi: Niech x∊L będzie dowolne, wówczas mamy, że: x∊(A∪B)^c ⇔ ¬x∊A∪B ⇔ ¬x∊A ∧ ¬x∊B ⇔ x∊A^c ∧ x∊B^c ⇔ x∊A^c∩ B^c ⇔ x∊P □

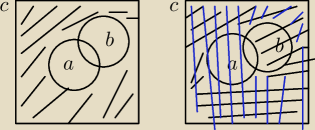
argh: nie wiem, czy można graficznie, jeśli tak, to na pierwszym rysunku przedstawiam (A∪B)^C. Na drugim kolorem czarnym zaznaczam A^C, a niebieskim B^C. Wówczas widzimy, że część wspólna to (A∪B)^C

wredulus_pospolitus: @argh ... wybacz, ale przedstawienie tego graficznie (w takiej formie) NIE JEST wystarczającym dowodem. Nie rozpatrując wszelkich możliwych sytuacji nie możesz jednoznacznie wykazać czy jest to prawdą czy też nie (wskazując jedynie jeden przypadek dla którego jest to prawda).

chichi: Obrazki to się w przedszkolu maluje