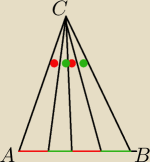
trójkąt oriana: Czy trzy odcinki mogą podzielić kąt ACB na dwie pary przystających kątów, a odcinek AB na dwie pary odcinków o równej długości, jak pokazano na rysunku (odpowiadające im przystające kąty odcinki o równej długości są pokazane w jednym kolorze)?

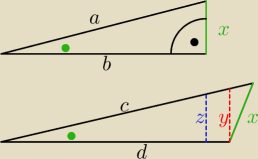
wredulus_pospolitus: Nie. Nie można. zakładając prawdziwość zauważamy: 1) Z tw. o dwusiecznej widzimy, że trójkąt ABC jest równoramienny (|AC| = |BC|) 2) związku z tym środkowy odcinek jest prostopadły do AB 3) bierzemy jeden ze środkowych odcinków (trójkąt prostokątny) oraz skrajny (trójkąt rozwartokątny) 4) zauważamy, że a < c oraz b < d (co można pokazać zaznaczając odpowiednie trójkąty prostokątne, gdzie przyprostokątną będzie a, przeciw prostokątną c ... i analogicznie z b i d)) 5) pozostaje pokazać, że y < x w tym trójkącie rozwartokątnym 6) a następnie pokazać, że z < y ... a przecież z = x z trójkąta prostokątnego sprzeczność

wredulus_pospolitus: ad. 5 można to pokazać poprzez szacowanie tw. cosinusów w trójkącie rozwartokątnym bądź poprzez obserwację gdzie tenże kąt rozwarty jest i co to oznacza