optymalizacja DAniel: W stożku o promieniu podstawy R i wysokości H zawarty jest graniastosłup prawidłowy czworokątny tak, że jego podstawa zawiera się w podstawie stożka. Jaką największą objętość może mieć ten graniastosłup?

chichi: A Pan @DAniel jak zwykle wrzuci zadanie i tylko czeka na gotowca, lepsze zimne piwo nad jeziorem, niż odrabianie za kogoś zadań domowych

Filip: Najaak

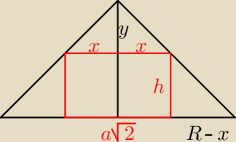
wredulus_pospolitus: y = H − h

	a√2
R−x = R −
	2

x		h		H
	=		=
y		R−x		R

stąd:

	Hy		a√2		H(H−h)		H(H−h)
x =		−−>		=		−−−> a =		√2
	R		2		R		R

	H(H−h)
V(a,h) = a2*h = (		√2)2*h = V(h)
	R

V'(h) = .... szukasz maksimum

daras: @chichi popieram w całej rozciągłości tylko.....jeziora brak

Filip: daras jak ocenissz szansze polskiej reprezentacji na euro 2021?