trapez kropka: Dany jest trapez 𝐴𝐵𝐶𝐷 o podstawach 𝐴𝐵 i 𝐶𝐷, w którym kąty 𝐵𝐴𝐷 i 𝐴𝐵𝐶 mają po 60 stopni oraz 𝐶𝐷 < 𝐵𝐶. Na boku 𝐵𝐶 tego trapezu wybrano taki punkt 𝐸, że 𝐸𝐵 = 𝐶𝐷. Wykazać, że odcinki 𝐵𝐷 i 𝐴𝐸 są równej długości.

chichi: Po przedłużeniu prostych zawierających ramiona tego trapezu równoramiennego znajdź trójkąty równoboczne i po zadaniu

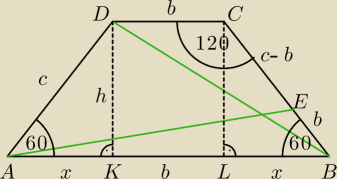
getin: w ΔADK i ΔLCB

	x
cos60o =
	c

1		x
	=
2		c

	1
x =		c
	2

|AB| = 2x+b = c+b z tw. cosinusów w ΔABE: |AE|² = |AB|² + |EB|² − 2*|AB|*|EB|*cos60^o

	1
|AE|2 = (c+b)2 + b2 − 2*(c+b)*b*
	2

|AE|² = c²+2b*c+b² + b² − b*c − b² |AE|² = b² + b*c + c² z tw. cosinusów w ΔBCD: |BD|² = |DC|² + |BC|² − 2*|DC|*|BC|*cos120^o

	1
|BD|2 = b2 + c2 − 2*b*c*(−		)
	2

|BD|² = b² + c² + b*c |AE|² = |BD|² więc |BD| = |AE|

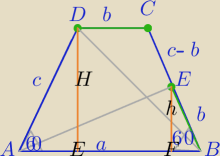
circle: ABCD− trapez równoramienny |BD=|AE| ? 1)

	a−b		a+b
|AE|=		, |EB|=
	2		2

	H
W ΔAED: tg60o=
	(a−b)/2

	a−b
H=		*√3
	2

	a+b		a−b
W ΔDEB: |BD|2=(		)2+(		*√3)2
	2		2

|BD|²=a²−ab+b² 2) W ΔABE: |AE|²=a²+b²−2*ab cos60^o=a²−ab+b² 3) |AE|=|DB| =======