 ogólnie to najkrótsza wysokość i najmniejsza dwusieczna wychodzą z największego kąta trójkąta
1) dla ostrokątnego
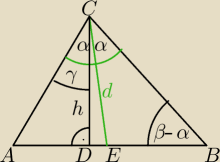
kąt ACB = 2α (największy kąt trójkąta)
d = |CE| najkrótsza dwusieczna
h = |CD| najkrótsza wysokość
zatem 2α>60o (bo największy kąt) oraz 2α<90o (bo ostrokątny)
więc α>30o oraz α<45o (inaczej 30o<α<45o)
ogólnie to najkrótsza wysokość i najmniejsza dwusieczna wychodzą z największego kąta trójkąta
1) dla ostrokątnego
kąt ACB = 2α (największy kąt trójkąta)
d = |CE| najkrótsza dwusieczna
h = |CD| najkrótsza wysokość
zatem 2α>60o (bo największy kąt) oraz 2α<90o (bo ostrokątny)
więc α>30o oraz α<45o (inaczej 30o<α<45o)
| h | 1 | |||
Trzeba udowodnić że | > | |||
| d | √2 |
| 1 | √2 | ||
= | |||
| √2 | 2 |
| h | ||
w ΔDEC: sinβ = | ||
| d |
| √2 | ||
Ponieważ | = sin45o, to trzeba pokazać że β > 45o i będzie udowodnione | |
| 2 |
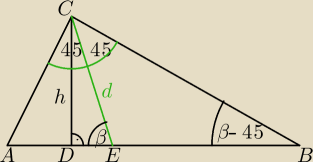 2) dla trójkąta prostokątnego (kąt ACB = 90o) czyli dla α = 45o
kąt EBC = β−α = β−45o
β−45o > 0o
β > 45o
udowodnione
2) dla trójkąta prostokątnego (kąt ACB = 90o) czyli dla α = 45o
kąt EBC = β−α = β−45o
β−45o > 0o
β > 45o
udowodnione
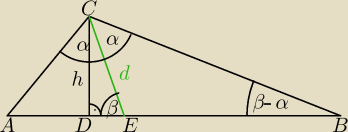 3) dla trójkąta rozwartokątnego
2α>90o
α>45o
β−α>0o
β>α
jeśli α>45o oraz β>α to β>45o
koniec dowodu dla Δ rozwartokątnego
3) dla trójkąta rozwartokątnego
2α>90o
α>45o
β−α>0o
β>α
jeśli α>45o oraz β>α to β>45o
koniec dowodu dla Δ rozwartokątnego