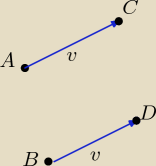
A = (x1, y1)
B = (x2, y2)
v = [a,b]
C = (x1 + a, y1 + b)
D = (x2 + a, y2 + b)
Izometria zachowuje odległość punktów, czyli powinno nam wyjść |AB| = |CD|
|AB| = √(x2 − x1)2 + (y2 − y1)2
|CD| = √(x2 + a − x1 − a)2 + (y2 + b − y1 − b)2 = √(x2 − x1)2 + (y2 − y1)2 = |AB|
Koniec. Tak mi się przynajmniej wydaje...
