Wyprowadzanie wzorów - przykład
gorgonek: Cześć! Czy wyprowadzanie wzorów może być częściowo słowne? Przykład:
Określenie liczby relacji zwrotnych
Na przekątnej wstawia się jedynki, a poza przekątną jest n2−n wolnych miejsc, które można
zapełnić zerami lub jedynkami na 2n2−n sposobów.
Czy ten przykład odzwierciedla wyprowadzenie tego wzoru? Byłbym zobowiązany za pomoc!
31 maj 11:42
ite:
Jaśniej będzie napisać:
Wszystkie pary o takim samym poprzedniku i następniku (na moim rysunku nr 1 są to pary z
przekątnej) należą do relacji zwrotnej z definicji, a więc wartość funkcji przynależności
wynosi dla każdej z nich 1. ←jeśli oczywiście o takiej funkcji wcześniej piszesz
Dla pozostałych par (na moim rysunku nr 1 wszystkie, które leżą poza przekątną) są dwie
możliwości: para należy lub nie do relacji. Taki par jest n2−n, stąd można je dołączyć lub
nie na 2n2−n sposobów, otrzymując tyle z tyle relacji zwrotnych.
Na pewno można to napisać lepiej, więc może jeszcze ktoś się wypowie.
31 maj 12:49
gorgonek:
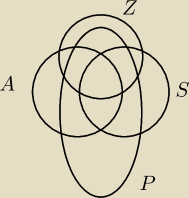
Rozumiem. A więc już wszystko się rozjaśniło, dziękuję uprzejmie.

Oczywiście, chętnie
również posłucham opinii innych osób.
Nie wiem, czy dobrze rozumiem, dla diagramu Venna 4−kołowego, ilość relacji należy policzyć
16−stoma różnymi wzorami? 16 wzorów wzięło się z faktu, że są to podzbiory danej przestrzeni,
gdzie A(antysymetryczna), Z(zwrotna), S(symetryczna), P(przechodnia).
Tak naprawdę, znane są jedynie wzory na ilość relacji:
− zwrotnych,
− symetrycznych,
− antysymetrycznych,
− przechodnich (brak jawnego wzoru, istnieje liczebność dla ciągu A006905 w bazie oeis org),
− zwrotnych i symetrycznych,
− zwrotnych i antysymetrycznych,
− symetrycznych i antysymetrycznych.
Można zatem zaznaczyć 6 obszarów spośród 16 podzbiorów (po podstawieniu za konkretną wartość
n−elementowego zbioru). Czy da się w jakiś sposób obliczyć pozostałe z podzbiorów(ich
dopełnień)?
31 maj 14:14
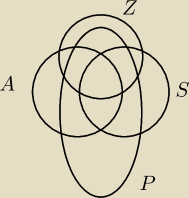 Rozumiem. A więc już wszystko się rozjaśniło, dziękuję uprzejmie.
Rozumiem. A więc już wszystko się rozjaśniło, dziękuję uprzejmie.  Oczywiście, chętnie
również posłucham opinii innych osób.
Nie wiem, czy dobrze rozumiem, dla diagramu Venna 4−kołowego, ilość relacji należy policzyć
16−stoma różnymi wzorami? 16 wzorów wzięło się z faktu, że są to podzbiory danej przestrzeni,
gdzie A(antysymetryczna), Z(zwrotna), S(symetryczna), P(przechodnia).
Tak naprawdę, znane są jedynie wzory na ilość relacji:
− zwrotnych,
− symetrycznych,
− antysymetrycznych,
− przechodnich (brak jawnego wzoru, istnieje liczebność dla ciągu A006905 w bazie oeis org),
− zwrotnych i symetrycznych,
− zwrotnych i antysymetrycznych,
− symetrycznych i antysymetrycznych.
Można zatem zaznaczyć 6 obszarów spośród 16 podzbiorów (po podstawieniu za konkretną wartość
n−elementowego zbioru). Czy da się w jakiś sposób obliczyć pozostałe z podzbiorów(ich
dopełnień)?
Oczywiście, chętnie
również posłucham opinii innych osób.
Nie wiem, czy dobrze rozumiem, dla diagramu Venna 4−kołowego, ilość relacji należy policzyć
16−stoma różnymi wzorami? 16 wzorów wzięło się z faktu, że są to podzbiory danej przestrzeni,
gdzie A(antysymetryczna), Z(zwrotna), S(symetryczna), P(przechodnia).
Tak naprawdę, znane są jedynie wzory na ilość relacji:
− zwrotnych,
− symetrycznych,
− antysymetrycznych,
− przechodnich (brak jawnego wzoru, istnieje liczebność dla ciągu A006905 w bazie oeis org),
− zwrotnych i symetrycznych,
− zwrotnych i antysymetrycznych,
− symetrycznych i antysymetrycznych.
Można zatem zaznaczyć 6 obszarów spośród 16 podzbiorów (po podstawieniu za konkretną wartość
n−elementowego zbioru). Czy da się w jakiś sposób obliczyć pozostałe z podzbiorów(ich
dopełnień)?