Dowód planimetria, kąty alfa i beta Kuku: Wykaż, że pole trójkąta, którego kąty mają miary α i β wyraża się wzorem P= r² * (tg ^α+β₂ )/( tg ^α₂*tg ^β₂ ) gdzie r oznacza promień okręgu wpisanego w ten trójkąt. Doszłam do tg ^α₂ = ^r_y tg ^β₂ = ^r_z tg ^α+2₂ = ^x_r Nie wiem czy to dobry trop, proszę o pomoc

πesio:

	r		r		α+β
y=		, z=		, x=r*tg
	α   tg   2		β   tg   2		2

P_Δ= r*p =r(x+y+z) podstawiaj dane

	α		β		α   β   tg +tg   2   2
i zastosuj wzór tg(		+		)=
	2		2		α   β   1−tg *tg   2   2

otrzymasz: ....................

	α   β   (tg +tg )   2   2
P= r2		=
	α   β   α   β   (tg *tg )(1−tg *tg )   2   2   2   2

	α   β   tg +tg   2   2		α+β
a to już teza ....... bo		= tg
	α   β   1−tg *tg   2   2		2

	α+β   tg   2
P= r2
	α   β   tg *tg   2   2

===============

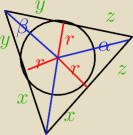
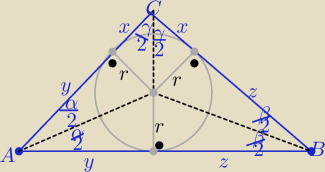πesio: korzystałam z oznaczeń jak na tym rysunku

	γ		α		β
α+β+γ=180o ⇒		=90o−(		+		)
	2		2		2

	γ		α+β		1
tg		= ctg		=
	2		2		α+β   tg( )   2

	α+β
dlatego x=r*tg
	2

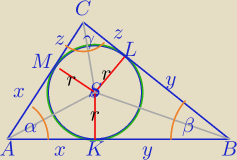Mila: P_Δ=p*r p=x+y+z, α+β+γ=180^o 1) Dla trzech kątów w Δ: α+β+γ=180^o Prawdziwa jest równość: (zobacz, czy jest w tablicach)

α

β

γ

α

β

γ

ctg

+ ctg

+ ctg

=ctg

*ctg

*ctg

2

2

2

2

2

2

2)

	α		x
ctg		=		⇔
	2		r

	α		β		γ
x=r*ctg		i y=r*ctg		i z=r*ctg
	2		2		2

3) α+β+γ=180 γ=180−(α+β)

γ		α+β		α+β		α+β
	=90−		⇔z=r*ctg(90−		)=r*tg
2		2		2		2

4)

α

β

γ

α

β

γ

PΔ=r*(r*ctg

+r*ctg

+r*ctg

)=r2*ctg

*ctg

*ctg

2

2

2

2

2

2

	α		β		α+β
PΔ=r2*(ctg		*ctg		*tg		)
	2		2		2

Jeśli nie wzoru w tablicach, to wg wskazówki πesia.

πesio: I za to Cię lubię

Mila: Ja Ciebie bardziej