K Kuba: 1. Mamy 5 klocków żółtych i 5 niebieskich. Na ile sposób można ułożyć z nich wieżę o wysokości 6 klocków? 2. Na ile sposobów możemy umieścić 20 cytryn w 4 numerowanych pudełkach, jeśli w każdym pudełku mają być conajmniej 2 cytryn. Z góry dziękuję za pomoc.

wredulus_pospolitus: 1) a jakie są możliwe podstawy tejże wieży ?

Kuba: To jest cała treść zadania, wiem, ze odpowiedź to 62, ale nie wychodzi mi to w żaden sposób

wredulus_pospolitus: 2. x₁ + x₂ + x₃ + x₄ = 20 (x₁−2) + (x₂−2) + (x₃−2) + (x₄−2) = 20 − 4*2 = 12 y₁ + y₂ + y₃ + y₄ = 12 i kombinacje z powtórzeniami się kłaniają (podstaw do wzoru)

Kuba: W 2 zadaniu poprawna odpowiedź to 455

wredulus_pospolitus: (1) zakładamy, że wykorzystujemy tylko 6 klocków które układamy jeden na drugi i w ten sposób uzyskujemy wspomnianą wieżę i na piechotę: 5 vs 1 <−−− 6 możliwości (x2) = 12

	6 2
4 vs 2 <−−−		= 15 możliwości (x2) = 30

	6 3
3 vs 3 <−−−		= 20 możliwości (x1) = 20

12+30+20 = 62 możliwości można by się kłócić, że przecież to nie są jedyne wieże (o wysokości 6 klocków) które można ułożyć z 10 klocków ... wystarczy po prostu użyć więcej klocków i położyć je obok

Kuba: Dzięki wielkie za pomoc

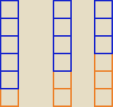
Mila: Klocki i wieże.

	6!		6!		6!
2*		+2*		+		{3!}=12+30+20=62
	5!		2!*4!		3!

Mila:

6!
	miało być na końcu sumy.
3!*3!

kerajs: 2⁶−2=62

Mila: Jak kto woli, do wyboru do koloru Jeden wzorek zawsze ładny.