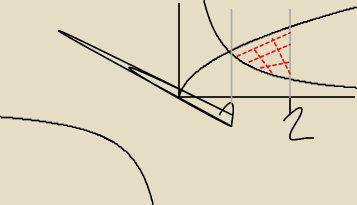
obszar normalny Łukasz: Mam do obliczenia pole danego obszaru ∫∫x²ydydx z D: y=√x y=1/x, x=2, x=1 Mój wynik to 11/8 Czy jakaś dobra dusza mogłaby sprawdzić, czy mój tok rozumowania jest dobry, co za tym idzie wynik też. Z góry dziękuję!

wredulus_pospolitus: jest ok

Mariusz: "Mam do obliczenia pole danego obszaru" To zastanów się co liczysz , no i przypomnij sobie jaka jest interpretacja całki podwójnej

an: Przecież bez całki oznaczonej, na "oko" widać, że to jest "ciutkę" większe 0,47, @wredulus czy to żart, czy

Filip: an, a to ZOBACZYLES/AS z RYSUNKU autora KEK?

Mariusz: @an Artur sprawdzał po prostu tylko czy on całkę podwójną poprawnie policzył nie zwracając uwagi na to co Łukasz ma policzyć Ta ja proponowałbym pole liczyć całką pojedynczą ale jeśli upiera się na całkę podwójną to powinien całkować jedynkę Z drugiej jednak strony x²y mogłoby być jakobianem pewnego przekształcenia tylko jakie to mogło być przekształcenie i jak zmieniały się oryginalne zmienne Gdybyśmy to wiedzieli to wiedzielibyśmy jakiego obszaru pole liczymy

Mariusz: @an ja uzyskałem wynik 1 − 0.47... ( Jak ty to pole liczyłaś(eś) )

Mila: ∫∫x²ydydx z D: y=√x y=1/x, x=2, x=1

	x2
1∫2[y=1/x∫√x(x2y)dy] dx=1∫2		[y2]1/x√x dx=
	2

	1		1		1
=		1∫2x2*(x−		) dx=		1∫2(x3−1) dx=
	2		x2		2

	1		1
=		[		x4−x]12=
	2		4

	1		1		11
=		*(4−2−		+1)=
	2		4		8

Jednak to nie jest pole obszaru. Pole obszaru licz tak jak pisze Mariusz.

Łukasz: Widzę, że wzburzyłem sporą dyskusję. Nie wiem sam do końca co miałem policzyć, możecie mi napisać jak wiecie. W zadaniu chodziło o to, że jest podana całka podwójna w zakresie D, a D jest wyznaczone przez wykresy danych funkcji. Na wykładzie mówiono na to obliczanie obszaru normalnego. Ja chciałem upewnić się, czy to co obliczyłem jest poprawne. Ale po obliczeniach osoby wyżej, widzę że zrobiłem to identycznie.

Łukasz: ale rzeczywiście nie jest to na pewno pole obszaru.

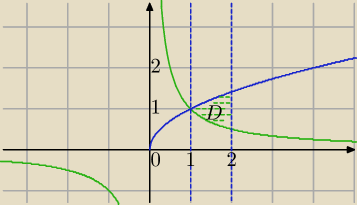
Mila: 1) No i dobrze zrobiłeś. Podany obszar jest normalny względem OX. 2) Obliczyłeś całkę podwójną gdzie obszar całkowania to D. 3) Gdyby trzeba było obliczyć pole tego obszaru ( D) to liczyłbyś całką pojedynczą ( może zrób to)

	1
S=1∫2(√x−		) dx
	x

albo całką podwójną taką: S= ∫ ∫ dydx D oblicz to pole na dwa sposoby.

Łukasz: Dziękuję!

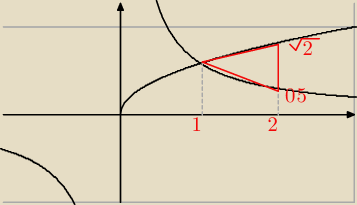
an: Do @Mariusz ja tu tylko chciałem powiedzieć, że pole tego czerwonego trójkąta policzone w pamięci ≈0,47 jest nieco mniejsze od pola liczonego obszaru i PAN student powinien to zauważyć, czyli wiedzieć, ze podana odpowiedź jest zła.

daras: PAN student? =Łukasz17:32, do końca sam nie wie co miał policzyć: więc napisał do wrózki

daras: D ≈ 0,53

wredulus_pospolitus: Pan student miał do obliczenia całkę z f(x,y) = x²*y po obszarze D. Jednak Pan student nie wiedział co tak naprawdę ma policzyć (jak to napisać), więc błędnie napisał, że chodzi o policzenie pola obszaru D. Jednak obliczenia wykonał dla policzenia objętości f(x,y) na obszarze D (bo tego chciał od niego prowadzący).

Mila:

daras: najważniejsze, ze tutejsi pomagacze wiedzieli o co chodzi i teraz student może zaprezentować "swoją" pracę dalej

Mila: Przecież policzył. Ja liczyłam i pisałam, bo w pamięci nie zdołałam.