Całka podwójna - objętość Tommy: Oblicz objętość bryły ograniczonej powierzchniami x²+y²=z², x²+y²=6−z Czy mógłby mi ktoś pokazać jak obliczyć to przy pomocy całki podwójnej ? Dziękuję bardzo

wredulus_pospolitus: Pytanie wstępne: czy wiesz jakie figury reprezentują te wzoru

Tommy: Wydaje mi się, że w obu przypadkach są to paraboloidy, przy czym x²+y²=z² jest chyba symetryczna względem płaszczyzny OxOy

wredulus_pospolitus: x⁺y² = z² −−−− dwa stożki symetryczne względem (0,0,0)

wredulus_pospolitus: Krok 1: Wyznaczasz obszar przecięcia się figur (z tego wyłuskasz obszar całkowania) Krok 2: Zauważasz, że jest to okrąg Krok 3: Stosujesz więc współrzędne ...... Krok 4 ∫∫_D (6 − x² − y²) − √x² + y² dxdy = .... dlaczego bo paraboloida sferyczna jest 'powyżej' stożka

Tommy: Właśnie największy problem mam z wyznaczeniem obszaru całkowania. Zamianę na współrzędne biegunowe i kolejne kroki rozumiem bez problemu ale to pierwsze sprawia mi największą trudność i nie wiem jak to zrobić

wredulus_pospolitus: x² + y² = z² ; x² + y² = 6−z −−−> z² = 6−z −−> z² + z − 6 = 0 −−−> (z+3)(z−2) = 0 zakładając, że chodzi o obszar dla z≥0 to mamy z=2 stąd: 'przecięcie' to okrąg x² + y² = 4 stąd obszar D: x² + y² ≤ 4

Tommy: Teraz już chyba wiem, o co chodzi. Dziękuję bardzo

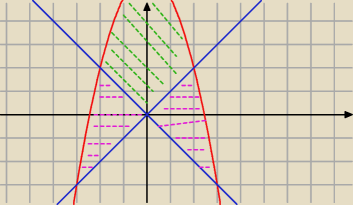
wredulus_pospolitus: czyli zielony obszar ... ale równie dobrze można policzyć fioletowy obszar

wredulus_pospolitus: zapewne układającemu zadanie chodziło o pierwszy (zielony) obszar tylko zapomniał dodać, że z≥0