punkty
Wol:
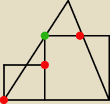
Dane są dwa kwadraty i trójkąt rownoramienny jak na rysunku. Wykaż że pukty zazanczone na
czerwo leżą na jednej prostej.
27 maj 11:51
Tadeusz:
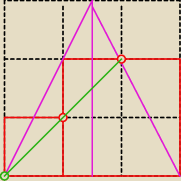
i wszystko jasne

27 maj 20:02
janek191:
W zadaniu są inne kwadraty.
Większy nie jest 2 razy większy od mniejszego.
27 maj 20:42
wredulus_pospolitus:
@Janek ... nie sugeruj się tym co narysował autor bo on nie narysował trójkąta równoramiennego

27 maj 21:20
wredulus_pospolitus:
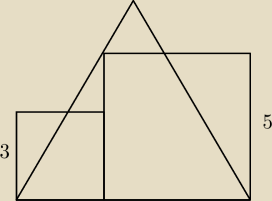
ale masz rację ... kwadraty nie muszą być w skali 1:2
27 maj 21:23
Wol: Tak nie sa w skali 1:2, a jak wykaz teraz?
28 maj 07:50
wredulus_pospolitus:
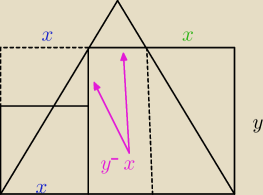
Sposób I:
x −−− bok mniejszego kwadratu
y −−− bok większego kwadratu
1) przedłużamy mniejszy kwadrat tak jak na rysunku
2) zauważamy przystawanie trójkątów prostokątnych (wystająca część dużego kwadratu, a drugi to
wystająca część dużego prostokąta −−− cecha chociażby B,K,B) stąd mamy
x
3) stąd mamy że te
y−x
4) przekątna kwadratu jest pod kątem 45
o ... odcinek łączący wierzchołek małego kwadratu z
przecięciem dużego z trójkątem także będzie pod tym kątem −−− trzy odcinki leżą na jednej
prostej
28 maj 10:16
wredulus_pospolitus:
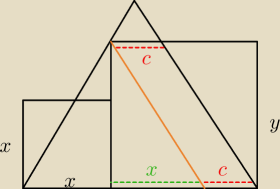
sposób II:
1) z lewego górnego wierzchołka dużego kwadratu prowadzimy równoległą do BC
2) z podobieństwa trójkątów wiemy że powstały trójkąt jest trójkątem równoramiennym, czyli bok
większego trójkąta jest jego wysokością i dzieli podstawę tegoż trójkąta na pół, stąd
x
3) stąd c = y−x
i argumentacja jak wcześniej
28 maj 10:20
an:
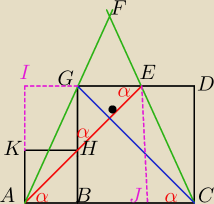
α= 45
o
Trójkąt równoramienny łatwo udowodnić, że ΔAGB i ΔAED są podobne, a więc AB=DE,
oraz GE=GH. Przekątna kwadratu AJEI Leży na tej samej prostej co przekątna AH
kwadratu ABHKΔ
cbdw.
28 maj 10:53
 Dane są dwa kwadraty i trójkąt rownoramienny jak na rysunku. Wykaż że pukty zazanczone na
czerwo leżą na jednej prostej.
Dane są dwa kwadraty i trójkąt rownoramienny jak na rysunku. Wykaż że pukty zazanczone na
czerwo leżą na jednej prostej.
 i wszystko jasne
i wszystko jasne 

 ale masz rację ... kwadraty nie muszą być w skali 1:2
ale masz rację ... kwadraty nie muszą być w skali 1:2
 Sposób I:
x −−− bok mniejszego kwadratu
y −−− bok większego kwadratu
1) przedłużamy mniejszy kwadrat tak jak na rysunku
2) zauważamy przystawanie trójkątów prostokątnych (wystająca część dużego kwadratu, a drugi to
wystająca część dużego prostokąta −−− cecha chociażby B,K,B) stąd mamy x
3) stąd mamy że te y−x
4) przekątna kwadratu jest pod kątem 45o ... odcinek łączący wierzchołek małego kwadratu z
przecięciem dużego z trójkątem także będzie pod tym kątem −−− trzy odcinki leżą na jednej
prostej
Sposób I:
x −−− bok mniejszego kwadratu
y −−− bok większego kwadratu
1) przedłużamy mniejszy kwadrat tak jak na rysunku
2) zauważamy przystawanie trójkątów prostokątnych (wystająca część dużego kwadratu, a drugi to
wystająca część dużego prostokąta −−− cecha chociażby B,K,B) stąd mamy x
3) stąd mamy że te y−x
4) przekątna kwadratu jest pod kątem 45o ... odcinek łączący wierzchołek małego kwadratu z
przecięciem dużego z trójkątem także będzie pod tym kątem −−− trzy odcinki leżą na jednej
prostej
 sposób II:
1) z lewego górnego wierzchołka dużego kwadratu prowadzimy równoległą do BC
2) z podobieństwa trójkątów wiemy że powstały trójkąt jest trójkątem równoramiennym, czyli bok
większego trójkąta jest jego wysokością i dzieli podstawę tegoż trójkąta na pół, stąd x
3) stąd c = y−x
i argumentacja jak wcześniej
sposób II:
1) z lewego górnego wierzchołka dużego kwadratu prowadzimy równoległą do BC
2) z podobieństwa trójkątów wiemy że powstały trójkąt jest trójkątem równoramiennym, czyli bok
większego trójkąta jest jego wysokością i dzieli podstawę tegoż trójkąta na pół, stąd x
3) stąd c = y−x
i argumentacja jak wcześniej
 α= 45o
Trójkąt równoramienny łatwo udowodnić, że ΔAGB i ΔAED są podobne, a więc AB=DE,
oraz GE=GH. Przekątna kwadratu AJEI Leży na tej samej prostej co przekątna AH
kwadratu ABHKΔ
cbdw.
α= 45o
Trójkąt równoramienny łatwo udowodnić, że ΔAGB i ΔAED są podobne, a więc AB=DE,
oraz GE=GH. Przekątna kwadratu AJEI Leży na tej samej prostej co przekątna AH
kwadratu ABHKΔ
cbdw.