f wymierne mm: Naszkicuj wykres funkcji f(x)=Ix−3I/x+1, a następnie naszkicuj wykres funkcji g, która każdej wartości parametru m przyporządkowuje liczbę równanie f(x)=m. Mam problem z tym zadaniem. Wydaję mi się, że wszystko robie dobrze, ale nie zgadzają mi się wyniki z odpowiedziami. Robię tak: D=R−{−1} dla x<3 − {−1} f(x)=⁴_x+1−1 dla x>/=3 f(x)= ⁻⁴_x+1+1 Wtedy rysuję te dwie funkcję, ale wyniki mam złę Moje wynik: dla m e (−oo;−3>u(1; oo) brak rozwiązań dla m e (−3;−1)u(−1;0) 1 rozwiązanie a w odpowiedziach jest: me<−1;0) brak rozwiązań m e(−oo;−1) u {0}u<1; oo) 1 rozwiązanie m e (0;1) 2 rozwiązania Wydaję mi się, że robię jakiś bład w przekształcaniu, ale nie wiem gdzie. Pomoże ktoś?

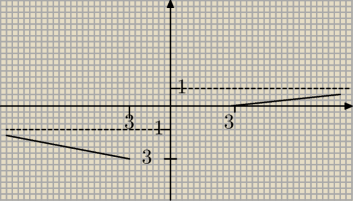
mm: taki mi wychodzi wykres. Oczywiście w 3 cwiartce te wartości są ujemne.

wredulus_pospolitus: a co ten wykres prezentuje ? bo NA PEWNO nie funkcję f(x)

mm: No właśnie taki mi wychodzi, oczyiście te proste nie są proste(po prostu nie umiem tutaj rysować). Mógłbyś wytłumaczyć, dlaczego to jest źle?

Gucio:

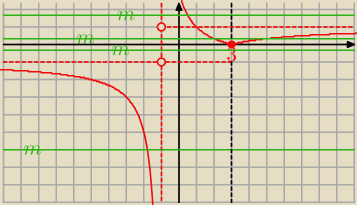
	|x − 3|		|x − 3|
Prawdopodobnie chodzi o f(x) =		, a nie o f(x) =		+ 1
	x + 1		x

	|x − 3|
Mamy y =		i y = m (to wykres funkcji stałej).
	x + 1

Wykres funkcji f(x)

	4		−4
dla x∊(−∞, −1)∪(−1, 3) y =		− 1, dla x∊<3, +∞) y =		+ 1
	x + 1		x + 1