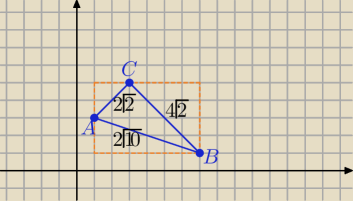
. Karol: Oblicz pole i obwód trójkata o wierzchołkach A =(1,3), B=97,1) i C= (3,5)

Karol: B= (7,1)

πqś:

Mariusz: Pole można dość łatwo policzyć wyznacznikiem Niech A= 1 3 1 7 1 1 3 5 1 det A = 1*(1*1−1*5)−3*(7*1−1*3)+1*(7*5−1*3) det A = 1*(−4)−3*4+1*32 det A = −16 + 32 det A = 16 2P = 16 P = 8 A jeśli chodzi o obwód to trzeba policzyć odległości między punktami i je dodać

πqś: ΔABC jest prostokątny

	1
P=		*2√2*4√2= 8
	2

Karol: A skąd się wzieły te pierwiastki z jakich obliczeń ?

Mariusz: trójkąt jest prostokątny (można to sprawdzić iloczynem skalarnym bądź korzystając z obliczeń πqsia i odwrotnego twierdzenia Pitagorasa)

chichi: 1/2 | |6 −2| | = 1/2(12+4) = 8, gdzie vec(AB)=[−6, 2] i vec(AC)=[2, 2] | |2 2| |

Mariusz: A =(1,3) B= (7,1) |AB|=√(7−1)²+(1−3)²=√6²+2²=√40 |AB|=2√10 analogicznie liczysz długości pozostałych boków

karol: a 4√81 i 2√81 to tak samo obliczyc z AB ?

Mariusz: karol długości pozostałych boków liczysz tak jak pokazałem dla boku AB

Filip: CZESC Mariusz