okregi
Patriszia Adams: zadanie nr 94
Przez punkt P lezacym na danym okrego poprowadzic styczna do okregu −to wiem
Zadanie nr 95
Dane sa dwa okregi C(O1,r1) i C(O2,r2) i odcinek o dlugosci r
Wykreslic okrag o promieniu r styczny do danych okregow
a)r1=40 r2=30 O1O2=90 r=20
b)r1=40 r2=60 O1O2=30 r=10
c) r1=20 r2=20 O1O2=20 i r=10
Chodzi o sama zasade jka to wykreslac
23 maj 22:24
a7:
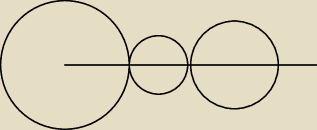
a)
23 maj 23:27
a7:
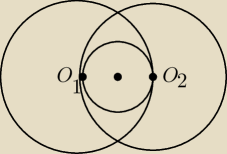
c)
23 maj 23:31
a:
a) źle O1O2= 110≠90
23 maj 23:39
a7:
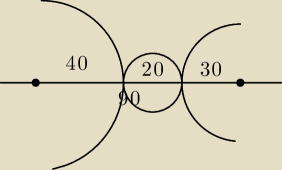
nie widzę innej opcji
23 maj 23:49
a:
a) r=20 a u Ciebie r=10
23 maj 23:51
I'm back:
@a7 − r=20 a nie d = 2r = 20

23 maj 23:51
a7: no niby tak, ale jak zrobić żeby okrąg był styczny do obu okręgów, i jednocześnie O1O2=90
23 maj 23:53
wredulus_pospolitus:
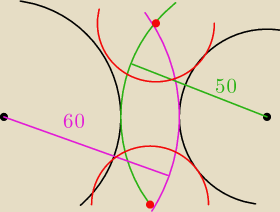
jak konstrukcyjnie to wykonać (posiadając cyrkiel i linijkę)
wyznaczamy środki wyjściowych okręgów i z nich tworzymy okręgi o promieniach r
1+r oraz r
2+r.
przecięcia = środek szukanego okręgu o promieniu r i stycznego do tychże dwóch okręgów
23 maj 23:57
wredulus_pospolitus:
@a7 −−− i (c) to nie jest jedyny taki okrąg ... mamy jeszcze dwa (zewnętrznie styczne) które
można wyznaczyć tak jak powyżej
23 maj 23:58
a7: no i sprawa jasna

24 maj 00:02
wredulus_pospolitus:
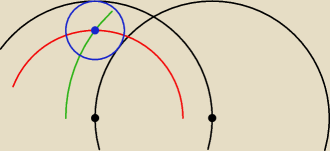
zewnętrznie styczne wyznaczamy poprzez łuki o promieniach r
1+r i r
2 + r (i patrzymy gdzie się
przecinają)
wewnętrznie styczne analogicznie: łuki o promieniach r
1−r i r
2−r (i znowu przecięcie daje
środek szukanego okręgu)
można jeszcze sprawdzić czy może być wewnętrznie styczny do jednego i zewnętrznie do drugiego
(przykład dla punktu (b) − niebieski okrąg)
24 maj 00:02
wredulus_pospolitus:
tfu ... to oczywiście dotyczy podpunktu (c) a nie (b)

24 maj 00:03
a:
24 maj 00:04
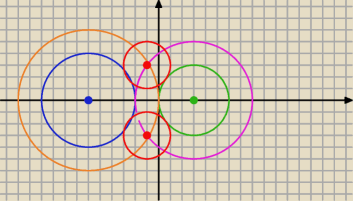
wredulus_pospolitus:
a więc dla punktu (c) będziemy mieć aż 7 takich okręgów:
i) 1 wewnętrznie styczny do obu
II) 2 zewnętrznie styczne do obu
III) 2 styczne zewnętrznie do lewego i wewnętrznie do prawego
IV) 2 styczne wewnętrznie do lewego i zewnętrznie do prawego (przykład − niebieski z 00:02)
24 maj 00:05
a:
Wrednusie r jest dane ( a nie dowolne

24 maj 00:06
wredulus_pospolitus:
ale ja Ciebie teraz nie rozumiem ... no jest dane 'r' i co związku z tym zmienia to co
napisałem ?
24 maj 00:10
a:
A ja Ciebie rozumiem

Nic nie zmienia .... jest ich
siedem 
24 maj 00:11
wredulus_pospolitus:
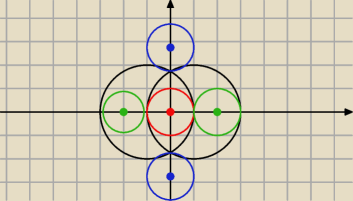
faktycznie ... (c) dla innego promienia (dużych okręgów) rozpatrywałem, jednak będzie tylko 5
okręgów

24 maj 00:15
24 maj 00:16
a:

24 maj 00:16
a:
Nawet "kratki" się przydały

24 maj 00:18
Patriszia Adams: Dziękuje.OMG az taki odzew.
a .Te konstrukcie mam w dwoch ksiazkach,bo Janowski nie pokazuje konstrukcji stycznych do
okregu
24 maj 06:05
Patriszia Adams: Ogolnie to pamietam ze taka konstrukcja byla u Krygowskiej ale juz nie chce mnie sie wyciagac
tej ksiazki
24 maj 06:12
wredulus_pospolitus:
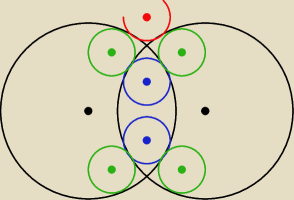
tak z ciekawości ... największa liczba szukanych okręgów to ... 8 (drugi czerwony nie zmieścił
mi się

24 maj 09:18
 a)
a)
 c)
c)
 nie widzę innej opcji
nie widzę innej opcji

 jak konstrukcyjnie to wykonać (posiadając cyrkiel i linijkę)
wyznaczamy środki wyjściowych okręgów i z nich tworzymy okręgi o promieniach r1+r oraz r2+r.
przecięcia = środek szukanego okręgu o promieniu r i stycznego do tychże dwóch okręgów
jak konstrukcyjnie to wykonać (posiadając cyrkiel i linijkę)
wyznaczamy środki wyjściowych okręgów i z nich tworzymy okręgi o promieniach r1+r oraz r2+r.
przecięcia = środek szukanego okręgu o promieniu r i stycznego do tychże dwóch okręgów

 zewnętrznie styczne wyznaczamy poprzez łuki o promieniach r1+r i r2 + r (i patrzymy gdzie się
przecinają)
wewnętrznie styczne analogicznie: łuki o promieniach r1−r i r2−r (i znowu przecięcie daje
środek szukanego okręgu)
można jeszcze sprawdzić czy może być wewnętrznie styczny do jednego i zewnętrznie do drugiego
(przykład dla punktu (b) − niebieski okrąg)
zewnętrznie styczne wyznaczamy poprzez łuki o promieniach r1+r i r2 + r (i patrzymy gdzie się
przecinają)
wewnętrznie styczne analogicznie: łuki o promieniach r1−r i r2−r (i znowu przecięcie daje
środek szukanego okręgu)
można jeszcze sprawdzić czy może być wewnętrznie styczny do jednego i zewnętrznie do drugiego
(przykład dla punktu (b) − niebieski okrąg)



 Nic nie zmienia .... jest ich siedem
Nic nie zmienia .... jest ich siedem 
 faktycznie ... (c) dla innego promienia (dużych okręgów) rozpatrywałem, jednak będzie tylko 5
okręgów
faktycznie ... (c) dla innego promienia (dużych okręgów) rozpatrywałem, jednak będzie tylko 5
okręgów 



 tak z ciekawości ... największa liczba szukanych okręgów to ... 8 (drugi czerwony nie zmieścił
mi się
tak z ciekawości ... największa liczba szukanych okręgów to ... 8 (drugi czerwony nie zmieścił
mi się 