Uzasadnij, ze dla każdej liczby x∈(−1;5) wyrażenie √4x^+12x+9+2√x^2−12+36 ma sta Wiktoria: Uzasadnij, ze dla każdej liczby x∈(−1;5) wyrażenie √4x²+12x+9+2√x²−12+36 ma stałą wartość. Złożyłam to do wzoru skróconego mnożenia, skróciłam pierwiastki i potęgi i mam: 2x+3+2x−12 Co teraz mam zrobić Nie rozumiem co mam zrobić z przedziałem, czy coś podłożyć? Co to w ogóle jest stała wartość?

Patriszia Adams: Ciekawe jak skrocilas pierwiastki i potegi?

wakacje: √4x²+12x+9=√(2x+3)²=|2x+3|=2x+3 √(x−6)²=|x−6|=−x+6 stąd: 2x+3+2(6−x)=2x+3+12−2x=15

Wiktoria: a co mówi mi 15? wyszła, ale jak wiedzieć, że to wartość stała z przedziału (−1,5)?

Wiktoria: co 15 udowodniła

ICSP: a co miałaś udowodnić? Cofnij się do polecenia.

Wiktoria: nie rozumiem logicznie tego

ICSP: Nie rozumiesz polecenia?

Wiktoria: tak, konkretnie tego przedziału, co on mi ma powiedzieć

ICSP: Masz pokazać, że nie ważne jaką liczbę weźmiesz z przedziału (−1 , 5) i podstawisz ją pod x w wyrażeniu: [4x² + 12x + 9} + 2√x² − 12x + 36 zawszy w wyniku otrzymasz taką samą liczbę. Przedział ten jest tylko po to aby po zredukowania wyrażenia do |2x + 3| + 2|x − 6| można było odpowiednio opuścić wartości bezwzględne tak aby x się skróciły.

Wiktoria: aa to już rozumiem, dziękuję bardzo

Filip: tutaj nie ma MOWY o SKRACANIU x, co najwyzej sie ZREDUKUJA panie ICSP

Adamm: najwyżej* ZREDUKUJĄ* Panie* oj Filipku Filipku

ICSP: Adamm nie karm trolla. Nie warto.

Filip: kek

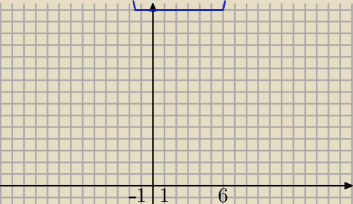
Mila: w(x)=|2x + 3| + 2|x − 6|=|2x+3|+|−2x+12|≥|2x+3−2x+12|=15 Równość zachodzi dla

	3
x∊<−		,6>
	2

	3		3
w(x)=15 dla x∊<−		,6> , ponieważ (−1,5)⊂<−		,6> to
	2		2

podane wyrażenie ma stałą wartość dla x∊(−1,5) i jest ta wartość równa 15.