Okregi
Patriszia Adams: dwa okregi C(O1,r) i C(O2,r) przecinaja sie w punktach M i N
Oznaczamy przez P punkt pierwszego okregu rozny od M i lezacy na srednicy O1M i przez Q
(Q≠M)punkt drugiego okregu lezacy na srednicy O2N
Udowodnic ze PQ=2O1O2
22 maj 21:15
Patriszia Adams:
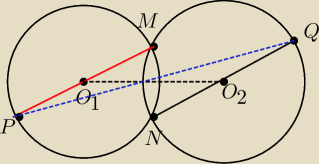
Dobry rysunek?
22 maj 22:02
Patryszia Adams:
22 maj 23:17
Patriszia Adams:
23 maj 10:42
ite: tak, rysunek jest poprawny
23 maj 12:41
Patriszia Adams: Jak teraz to udowodnic?
23 maj 12:49
ite:
Ja się nie podejmę, bo wg mnie |PQ|>2|O1O2|.
Ale może się mylę i Panie moderatorki mnie poprawią.
23 maj 13:20
Patriszia Adams: Ok Nie ma sprawy
23 maj 14:02
Gucio:

23 maj 16:46
ite:
Guciu 
23 maj 16:53
Patriszia Adams: @ Gucio kimkolwiek jestes prosze jakis komentarz
Stokrotne dzięki
23 maj 18:03
Patryszia Adams:
23 maj 20:58
a7:
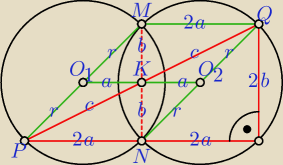
nie jestem wprawdzie Guciem, ale chodzi pewnie o to, że
PQ jest przeciwprostokątną trójkąta prostokątnego, w którym jedna z przyprostokątnych ma
długość 4a czyli 2O1O2
czyli |PQ|>2|O1O2|, jak zauważyła ite (przeciwprostokątna jest dłuższa niż każda z
przyprostokątnych)
23 maj 21:12
Patriszia Adams: Treśc zadania jest dobra .Jeszcze raz sprawdzilem
Oprocz tego polecenia bylo jeszce jednio a mianoicie udowodnic ze punkty PNQ sa wspolliniowe
23 maj 21:26
Agatka:
Przeczytaj jeszcze raz dokładnie treść zadania, to pogadamy
Przy takiej treści punkty PNQ nie są współliniowe !
23 maj 21:36
Patriszia Adams:
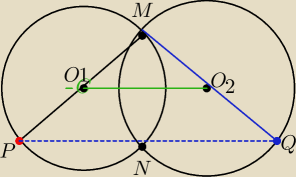
Tresc jest taka jak napisalem
Pewnie w tresci jest blad .Teraz jest dobrze tak jak na rysunku .Wiec w tresci powinno byc
(punkt Q lezy na srednicy
O
2M
PO udowodnieniu ze PNQ sa wspoliniowe mozna byloby skorzystac z tego ze O
1O
2 jest linia
srodkowa trojkata PMQ
A jak inaczej mozna gdyz tego o lini srodkowej trojkata jeszce nie bylo?
23 maj 21:56
Patriszia Adams: Do udowodnienia ze punkty PNQ sa wspoliniowe skorzystalem z tw o mierze kąta wpisanego opartego
na srednicy
Ale tez tego twierdzenia jeszcze nie bylo
23 maj 22:00
Agatka:
Czworokąty PNO2O1 i QNO1O2 są przystajacymi równoległobokami
23 maj 22:08
Patriszia Adams: I co tym udowodnimy?
Musze miec wytlumaczone prosto.Naprawde . Prosze sie nie obrazac na to
23 maj 22:14
a:
Wszystko

24 maj 00:22
a:
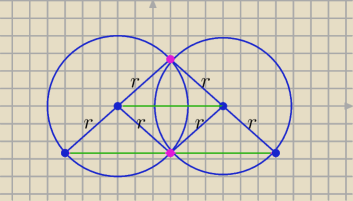
24 maj 00:32
Patriszia Adams: Tak najlepiej wszystko po kolei
24 maj 06:07
 Dobry rysunek?
Dobry rysunek?



 Tresc jest taka jak napisalem
Pewnie w tresci jest blad .Teraz jest dobrze tak jak na rysunku .Wiec w tresci powinno byc
(punkt Q lezy na srednicy
O2M
PO udowodnieniu ze PNQ sa wspoliniowe mozna byloby skorzystac z tego ze O1O2 jest linia
srodkowa trojkata PMQ
A jak inaczej mozna gdyz tego o lini srodkowej trojkata jeszce nie bylo?
Tresc jest taka jak napisalem
Pewnie w tresci jest blad .Teraz jest dobrze tak jak na rysunku .Wiec w tresci powinno byc
(punkt Q lezy na srednicy
O2M
PO udowodnieniu ze PNQ sa wspoliniowe mozna byloby skorzystac z tego ze O1O2 jest linia
srodkowa trojkata PMQ
A jak inaczej mozna gdyz tego o lini srodkowej trojkata jeszce nie bylo?

