 W trójkącie prostokątnym równoramiennym ABC przyprostokątne mają długość √2 : Punkty D, E
należą do przeciwprostokątnej AB oraz kąt acd= kąt dce = kąt ecb Oblicz długości odcinków AD,
DE, EB.
W trójkącie prostokątnym równoramiennym ABC przyprostokątne mają długość √2 : Punkty D, E
należą do przeciwprostokątnej AB oraz kąt acd= kąt dce = kąt ecb Oblicz długości odcinków AD,
DE, EB.
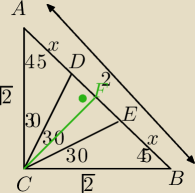 z tw. Pitagorasa AB=2
wysokość DF=1 (gdyż pole ABC=1/2*√2*√2=1 czyli 1/2*AB*DF=2 czyli DF=1)
PΔABC=1=PΔADC+PΔDEC+PΔBEC
DC=CE=z
1/2*√2*zsin30+1/2*z2*sin30+1/2*√2*z*sin30=1
Δ=24 √Δ=2√6
z=√6−√2
AD=EB=x
PΔADC=1/2x*1=1/2√2*z*sin30 ⇒ x=√3−1
DE=y=2−2x=2−2(√3−1)=4−2√3
z tw. Pitagorasa AB=2
wysokość DF=1 (gdyż pole ABC=1/2*√2*√2=1 czyli 1/2*AB*DF=2 czyli DF=1)
PΔABC=1=PΔADC+PΔDEC+PΔBEC
DC=CE=z
1/2*√2*zsin30+1/2*z2*sin30+1/2*√2*z*sin30=1
Δ=24 √Δ=2√6
z=√6−√2
AD=EB=x
PΔADC=1/2x*1=1/2√2*z*sin30 ⇒ x=√3−1
DE=y=2−2x=2−2(√3−1)=4−2√3
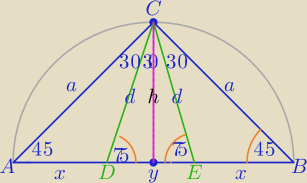 a=√2
1) |AB|=a√2=√2*√2=2
h=1
a=√2
1) |AB|=a√2=√2*√2=2
h=1
| 1 | ||
PΔABC= | *2*1=1 | |
| 2 |
| 1 | 1 | |||
PΔABC= | *(a*dsin30o+d2*sino+adsin30o)= | *(√2d+d2+√2d) | ||
| 2 | 4 |
| 1 | |
*(√2d+d2+√2d)=1 | |
| 4 |
| x | d | ||
= | |||
| sin30 | sin45 |
| √2 | 1 | |||
x* | =(√6−√2)* | |||
| 2 | 2 |




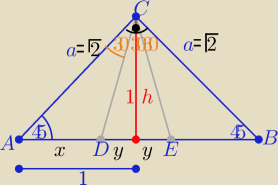 Można też tak:
Można też tak:
| a2 | ||
2P(ΔADC) = | i 2P(ADC)=x*h=x , bo h=1 | |
| ctg45o+ctg30o |
| 1 | ||
to | = √3−1 =x | |
| 1+√3 |