Zadanko ze sprawdzianu. Potrzębuję jak najszybciej. Z góry dzięki Kevo: Dwusieczna kąta prostego BAC w trójkącie ABC przecina przeciwprostokątną w punkcie D. Bok AB jest o 7 dłuższy od boku AC, a różnica między obwodem trójkąta ABD i trójkąta ACD jest równa 12. Oblicz różnicę między długościami okręgów opisanych na trójkącie ABD i ACD. Pliz na juuuuż

chichi: Nie no facet nie przeginaj

chichi:

	5√2
Bardzo na szybko robione więc może być błąd obliczeniowy, ale mam, że R1−R2=
	2

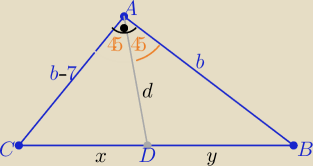
figa: Z treści zadania : L₂(ABD)>L₁(ACD) to b+d+y −x−d−b+7=12 ⇒ y−x=5 , y>x z tw. sinusów

	x		y
2R1=		i 2R2=		, y>x to R2>R1
	sin45o		sin45o

	y		x		y−x		5
R2−R1=		−		=		=
	√2		√2		√2		√2

	5√2
R2−R1=
	2

=============

chichi: Już dawno po sprawdzianie

figa: Będzie dla "potomnych"