styczna ~~greg: punkty A, B, C leżą na okręgu o promieniu r i o środku S. Styczna do okręgu w punkcie A przecina prostą BC w punkcie P. Oblicz promień tego okręgu, jeśli PC=PB=2√3 oraz |PS|=12. Przeciez to nielogiczne zeby PC=PB

a7: no chyba tak, może literówka, nie ma jakiejś erraty?

~~greg: nie ma, kombinuje ale przeciez to nie da sie narysowac

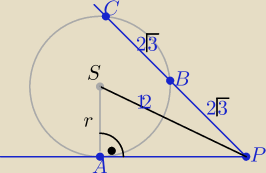
krasnoludek: Myślę że powinno być: BC=PB Z tw. o stycznej i siecznej : |AP|²=|PC|*|BP| ⇒ ........ |AP|² = 24 z tw. Pitagorasa w ΔASP r²=12²−24 r=........

~~greg: też tak myślę

~~greg: JEST OK bedzie to prosta równoległa do srednicy, tak mi sie wydaje

~~greg: nie, jednak jest zle

a7: a ile powinno wyjść?

chichi: W zadaniu jest zapewne literówka, a rozwiązanie @krasnoludek jest poprawne