Hiperbola własności
Valeriano : Dlaczego hiperbola jest „niemalejąca” w przedziale R/[0]? Jak to jest możliwe? Przecież
definicja mówi ze funkcja jest niemalejąca <=> jeśli x1<x2 oraz f(x1)<lub=f(x2).
18 maj 19:18
a7:
18 maj 19:22
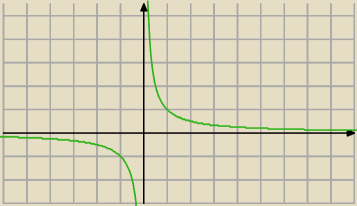
a7: y=1/x
18 maj 19:23
a7: ale jaką hiperbolę Ty masz na myśli, bo ta którą widać na powyższym rysunu jest raczej
przedziałami malejąca...
18 maj 19:24
18 maj 19:56
18 maj 19:57
Valeriano : Właśnie chodzi mi o zwykłą y=1/x, dokładnie tak jak napisałem, jest napisane w podręczniku
18 maj 21:08
a7: może pomyłka w podręczniku?
18 maj 21:10
Valeriano: Ze niby jest niemalejąca w przedziale (−∞;0)u(0;+∞)
18 maj 21:12
Valeriano: Poczekaj dokładnie ci przepisze
18 maj 21:12
ABC: po pierwsze jest malejąca , po drugie w każdym z przedziałów ale nie w całej dziedzinie
18 maj 21:13
Valeriano: „Uwaga: Zauważ ze funkcja f(x)=1/x nie jest malejąca w zbiorze (−∞;0)u(0;∞) „ tak jest napisane
18 maj 21:14
a7: w którym podręczniku?
18 maj 21:15
a7: jest malejąca nie w zbiorze tylko na przedziałach, może o to chodzi
18 maj 21:15
ICSP: "Niemalejąca" to nie to samo co "nie jest malejąca".
Najpierw zastanów się co piszesz.
18 maj 21:16
Valeriano: Nowa era 2, rozszerzenie, 2015 rok, strona 73
18 maj 21:16
a7: no to może właśnie o to chodzić, że nie jest malejąca w zbiorze, tylko jest malejąca na
przedziałach/przedziałami
18 maj 21:19
ABC: ja uczę z tej książki , wszystko tam jest dobrze napisane , że jest malejąca w każdym z
przedziałów
a nie jest w całej dziedzinie
18 maj 21:45
