sześcian
Brat: Oblicz, stosując twierdzenie Pitagorasa długość przekątnej sześcianu o boku a.
3 mar 19:35
damian:
a − krawędź sześcianu
a√2 − przekątna ściany sześcianu (przekątna kwadratu)
x − przekątna sześcianu
x2 = a2 + (a√2)2
x2 = 3a2
x = a√3
3 mar 19:38
Noah:
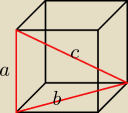
b=a
√2 to wiesz z wlasnosci przekatnej kwadratu no a c liczymy od pitka
c
2=a
2+b
2
c
2=a
2+2a
2
c
2=3a
2
c=
√3a2
c=a
√3
3 mar 19:41
Brat: Dzięki piękne
3 mar 19:43
Eta:
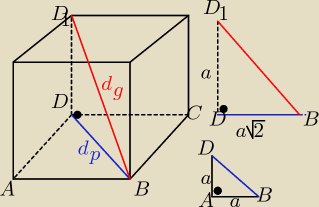
z ΔABD z tw. Pitagorasa:
IDBI
2= a
2+a
2= 2a
2 => IDBI= d
p = a
√2
z ΔDBD
1 z tw. Pitagorasa:
IBD
1I
2= a
2+IDBI
2
IBD
1I
2= a
2 +2a
2= 3a
2
IBD
1I= d
g=
a√3 [j]
3 mar 19:50
Brat: Śliczne dzięki
3 mar 19:52