Dziedzina, trygonometria, logarytm
Szkolniak: Jakie wartości x z przedziału <0;2π> należą do dziedziny funkcji y=
√log(cosx+|cosx|)
| | π | | 5 | |
Finalnie wychodzi mi przedział x∊(0; |
| >∪< |
| π;2π), a w odpowiedzi zawarte jest w tym |
| | 3 | | 3 | |
przedziale również 0 oraz 2π, stąd moje pytanie − skąd te liczby?
Określam warunki na dziedzinę (zajmę się tylko jednym z warunków, bo zakładam że z niego wynika
ten problem):
log(cosx+|cosx|)≥0 ∧ cosx+|cosx|>0
Zajmę się tym drugim:
cosx+|cosx|>0 ... i teraz rozbijam sobie to tak:
v
No i z tego tak naprawdę otrzymuje warunek, że cos(x)>0, z którego już wypadają x=0 oraz x=2π,
więc o co chodzi? Gdzie mam błąd?
13 maj 23:32
chichi:
Zrób wykres takiej funkcji, a się przekonasz

| | ⎧ | 2cos(x), cos(x)≥0 | |
| f(x)= | ⎩ | 0, cos(x)<0 |
|
13 maj 23:46
Szkolniak: Zrobiłem wykres w geogebrze i to widzę, ale dlaczego to nie wynika z algebraicznego
rozwiązania, z nierówności? Nie widzę żadnego momentu gdzie zrobiłbym jakieś niepoprawne
przejście..
13 maj 23:50
ICSP: Dlaczego z warunku cosx > 0 wypadają x = 0 oraz x = 2π?
Możesz to jakoś uargumentować?
14 maj 00:46
chichi:
Słabo patrzył na wykres, o którym mówiłem

14 maj 00:53
Szkolniak: Rzeczywiście, wiąże się to po prostu z okresowością funkcji y=cos(x)?
Rozwiązując te nierówności nie myślałem aż tak dogłębnie, działałem po prostu na podobnej
zasadzie jakbym miał takie nierówności:
| | ⎧ | x−5>0 | |
| | ⎩ | x−5≥0 | , a z tego oczywiście mamy, że x>5
|
14 maj 01:02
chichi:
Ty chyba patrzysz cały czas na wykres sinusa..

14 maj 01:04
chichi:
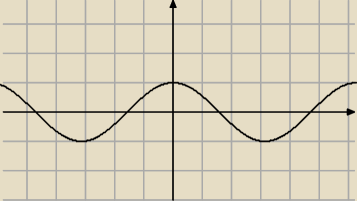
14 maj 01:05
ICSP: Argumentacja zakończona znakiem zapytania jest bardzo złą argumentacja.
Już na wstępie pokazujesz drugiej stronie, że nie do końca wiesz o czym mówisz.
14 maj 01:06
Mila:
Szkolniak wszystko jasne, czy pisać całe rozwiązanie?
14 maj 22:52
chichi:
@
Mila a gdzie wyparowało twoje rozwiązanie?

14 maj 23:40
Mila:
Wyparowało, bo kopiowałam i na końcu, nie poprawiłam jak trzeba.
Tak się mści lenistwo.
Wystarczy Twoje wyjaśnienie

14 maj 23:48
chichi:
@
Mila też bym chciał mieć takie moce hah

15 maj 00:04
Mila:
Zawsze mogę pomóc w tej sprawie

15 maj 00:08
chichi:

15 maj 00:10
chichi:
@
Mila kojarzysz może 'Geometria analityczna w zadaniach' E. Kącki D. Sadowska L.
Siewierski, jeśli tak to prosiłbym Cię o opinię tej pozycji, bo planuję wypożyczyć

15 maj 00:12
Szkolniak: Mila szkoda czasu aby pisać całe rozwiązanie, miałem pytanie jedynie o pewien fragment,
reszta zrozumiała.. Jednak dziękuję pięknie że pytasz!

20 maj 00:26










