GEOMETRIA nawaleta: W trójkacie ABC w któym |CA|=|CB|=10 i kąt ABC=7, obrano punkt D na boku AB taki, że AD=2*DB. Oblicz odległosc punktu D od boków CA i CB tego trójkata. Mam tutaj problem z podobienstwem, bo jest tego podobienstwa sporo

6latek: Najpierw sprawdz tresc zadania Kąt ABC=7*57⁰≈400^o

nawaleta: powinno być 70 stopni

chichi: Na waleta − odważnie Nie zapominaj, że masz jeszcze różne wzory na pole trójkąta

nawaleta: Nie rozumiem chyba

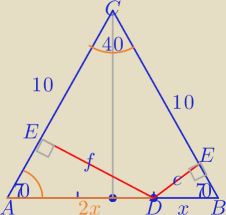
Mila: W trójkącie ABC w którym |CA|=|CB|=10 i kąt ABC=70^o, obrano punkt D na boku AB taki, że AD=2*DB. Oblicz odległość punktu D od boków CA i CB tego trójkąta. 1)

AD		2
	=
DB		1

ΔAED∼ΔBED w skali k=2 f=2e

	e
sin70=		⇔e=x*sin700
	x

2) W ΔABC:

3x		10
	=		⇔3x*sin70o=10*sin40o
sin40		sin70

	10sin40o
(x*sin(70o)=
	3

3)

	10sin40o
e=
	3

	20sin40o
f=
	3

=============

myszka Miki: Korzystam z rys. Mili P(ABC)=50*sin40^o i f=2e

	1		1
P1=		2e*10= 10e , P2=		*e*10 = 5e
	2		2

P=P₁+P₂=15e

	10		20
15e=50sin40o ⇒ e=		sin40o i f=2e=		sin40o
	3		3

=========================

chichi: Właśnie takie rozwiązanie miałem na myśli wspominając o polach

ϱoco: Trzeba dorysować odcinek CD.

chichi: Jak ktoś tego nie widzi, to niech sobie dorysuje..

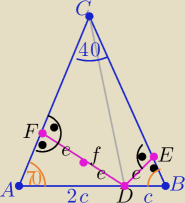
πesio: P₁=P_ADC , P₂=P_DBC Czy teraz pasuje ? .. ocoϱ

Rumcajs: