funkcja Kuba: witam, mam takie zadanie i nie umiem go rozwiązać. Chorowałem długo a to co przesyłają zdalnie nie wchodzi mi w ogóle .Gdyby Ktoś mógł mi pomóc, to zadanie z liceumi trzeba coś tam wyliczać z delty proszę i z góry dziękuję natysuj wykres funkcji i opisz jej własności f(x)=.1− wartośc bezwzględna x²−1

Szkolniak: f(x)=1−|x²−1|

	⎧	1−x2+1, gdy x2−1≥0
f(x)=	⎩	1+x2−1, gdy x2−1<0

	⎧	−x2+2, gdy x∊(−∞;1>∪<1;+∞)
f(x)=	⎩	x2, gdy x∊(−1;1)

1) dziedziną funkcji jest zbiór liczb rzeczywistych 2) zbiorem wartości funkcji jest przedział (−∞;1> 3) funkcja nie przyjmuje wartości najmniejszej, wartość największa równa 1 dla x∊{−1,1} 4) nie jest różnowartościowa 5) funkcja jest parzysta itd...

Kuba: no ok, ale babka kazała rozwiązać to z deltą , x1 i x2, wierzchołkiem p,q i narysować

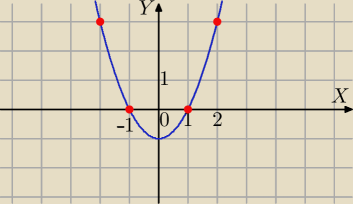
Mila: f(x)=1−|x²−1| 1) Rysuję wykres funkcji: g(x)=x²−1 2) Symetria tej części wykresu, która leży pod OX względem osi OX to narysuję w następnym wątku. otrzymasz wykres funkcji: s(x)=|x²−1|

Szkolniak: Wydaje mi się że delta czy wierzchołek to niepotrzebne do narysowania wykresu funkcji y=x² w przedziale (−1;1).. y=x² x₀=0 oraz W=(0,0) Co do y=−x²+2, to Δ=8=(2√2)²

	0−2√2		0+2√2
⇒ x1=		, x2=
	−2		−2

Można też po prostu: f(x)=0 ⇔ (x²=0 ∧ x∊(−1;1)) v (−x²+2=0 ∧ |x|≥1) x∊{−√2,0,√2} Daj znać czy o to Ci chodzi?

Kuba: Mila, droga wybawczyni, a nie trzeba liczyć delty ,p,q

Kuba: szkolniaku, Ty rozwiązujesz na wyższym poziomie niż ja........... ja muszę to zrobić jakoś łatwiej, 2 liceum

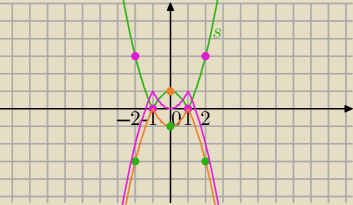
Mila: 3) s(x)=|x²−1| 4) symetria wykresu funkcji s(x) względem osi OX⇒otrzymujesz wykres funkcji : h(x)=−|x²−1| 5) Przesuwasz wykres funkcji h(x) o jedną jednostkę do góry⇒otrzymujesz wykres funkcji: f(x)=−|x²−1|+1 Własności: 1) spróbuj sama

Szkolniak: W takim razie zajmę się osobno tymi dwoma funkcjami: (1) to y=x² (2) to =−x²+2 (1) y=x² (a=1, b=0, c=0)

	−b		0
p=		=		=0
	2a		2

q=f(p)=f(0)=0, zatem nasz wierzchołek ma współrzędne W=(0,0) Teraz miejsca zerowe: f(x)=0 x²=0 x=0, pamiętając, że wykres funkcji jest ograniczony do przedziału (−1;1) (2) y=−x²+2 (a=−1, b=0, c=2)

	−b		0
p=		=		=0
	2a		−2

q=f(p)=f(0)=2, zatem W=(0,2), ale zauważ że teraz dziedziną funkcji jest przedział (−∞;−1>∪<1;+∞), czyli wierzchołka tak naprawdę nie rysujemy W takiej sytuacji obliczyłbym wartości funkcji y=−x²+2 w punktach x=−1 oraz x=1 f(−1)=−1+2=1 f(1)=−1+2=1 No i teraz gdybyś chciał wyznaczyć miejsca zerowe, to oczywiście: −x²+2=0 x²=2 ∧ x∊(−∞;−1>∪<1;+∞) x∊{−√2,√2} To może teraz bardziej zrozumiale?

chichi: (1) (2) (3) (4) x² → x²−1 → |x²−1| → −|x²−1| → −|x²−1|+1 (1) Przesunięcie o wektor v=[0, −1] (2) Symetria częściowa względem osi OX (to co pod osią odbijamy nad) (3) Symetria całościowa względem osi OX (4) Przesunięcie o wektor u=[0, 1]

chichi: O @Mila była szybsza

Kuba: Mila dziękuję bardzo, poleciła Mi Was moja koleżanka, która dzięki Waszym tłumaczeniom podciągnęła się w tamtym roku. Jaszcze raz wielkie dzięki

Kuba: dziękuję Wam wszystkim, jak mi wytłumaczyliście to wiem jak robić następne przykłady, już chyba sam dam radę buziaki i pomagajcie dalej innym dzięki

Mila: Wpisuj zadania w razie kłopotów