trójkąt szymon: Boki trójkata mają długości 13,14,15 Oblicz długość okręgu,którego środek leży na najdłuższym boku trójkąta i który jest styczny do dwóch pozostałych boków trójkąta

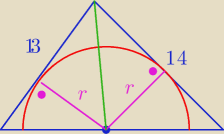
janek191: Z wzoru Herona obliczamy pole trójkąta P = 84 j² Oraz P = 0,5 *13 r + 0,5*14 r = 13,5 r więc 13,5 r = 84

	2
r = 6
	9

==========

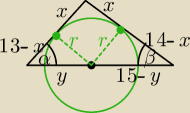getin: z tw. cosinusów

	33
142 = 132+152−2*13*15*cosα → cosα =
	65

	21
132 = 142+152−2*14*15*cosβ → cosβ =
	35

z trójkątów prostokątnych

	13−x
cosα =
	y

	14−x
cosβ =
	15−y

13−x		33
	=
y		65

14−x		21
	=
15−y		35

33y = 65(13−x) 21(15−y) = 35(14−x)

	28
x =
	3

	65
y =
	9

r² + (13−x)² = y²

	11		65
r2 + (		)2 = (		)2
	3		9

	56
r =
	9

	112
Obw = 2π*r =		π
	9

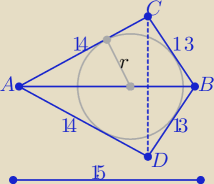gargamel: P(deltoidu)ACBD=2P(ΔABC) ze wzoru Herona P(ABC)=√21*7*6*8= 84 P(deltoidu)=P_d= 168

	168		56
Pd=rp ⇒ r=		=
	27		9

L_o=2πr

	112
Lo=		π
	9

=============

gargamel: Sorry Janek Nie widziałem Twojego wpisu Zauważyłem jedynie "rozlazłe"..... rozwiązanie getin