analityka Ola: Dane są punkty A(4, 2), B(8, 8) oraz prosta k: 5𝑥−𝑦−12=0. Znajdź na prostej k wszystkie takie punkty C, żeby kąt ACB był prosty.

wredulus_pospolitus: Wskazówka: Ola −−− jaka jest zależność pomiędzy trójkątem prostokątnym a okręgiem na nim opisanym? To załatwi kwestie AB jako przeciwprostokątna Natomiast przypadek gdy AB jest przyprostokątną (o ile może nią być) −−− prowadzić prostopadłe do AB z punktu A (a później z punktu B) i sprawdzasz gdzie przecina prostą k

Ola: a jaśniej?

wredulus_pospolitus: ale co 'jaśniej' SPRAWDŹ temat; trójkąt prostokątny wpisany w okrąg

wredulus_pospolitus: łeee ... ACB na być prosty ... więc tylko trzeba narysować okrąg i masz wyznaczone punkty (ewentualnie będzie trzeba je wyznaczyć z układu równań)

ICSP: C(x , 5x − 12) CA = [4 − x , 14 − 5x] CB = [8 − x , 20 − 5x] <CA , CB> = 0 (4−x)(8−x) + (14 − 5x)(20 − 5x) = 0 x = 3 v x = 4 C(3,3) , C(4,8)

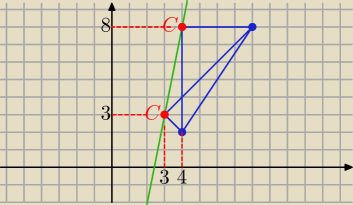
gargamel: k: y= 5x−12 C(x, 5x−12) z warunku prostopadłości wektorów AC⊥BC → AC=[x−4,5x−14] → BC=[x−8, 5x−20] (x−4)*(x−8)+(5x−14)(5x−20)=0 .................. x²−7x+12=0 ⇒ (x−3)(x−4)=0 x=3 v x= 4 y=3 v y=8 C(3,3) lub C(4,8) =============

wredulus_pospolitus: (x−6)² + (y−5)² = 13 y = 5x − 12 (x−6)² + (5x − 17)² = 13 x² − 12x + 36 + 25x² − 170x + 289 = 13 26x² − 182x + 312 = 0 13x² − 91x + 156 = 0 x = 3 −−> y = 3 x = 4 −−−> y = 8

gargamel: x²−7x+12=0