geometria analityczna
Ola: Zbadaj położenie okręgów (x +2)2+(y −2)2 = 4 i x2 + 10x + y2 – 4y + 25 = 0.
12 maj 22:02
chichi:
O
1: (x+2)
2+(y−2)
2=4 ⇒ S
1=(−2, 2) ∧ r
1=2
O
2: (x+5)
2+(y−2)
2=4 ⇒ S
2=(−5,2) ∧ r
2=2
|O
1O
2|=3
r
1−r
2 = 0 < 3 < 4 = r
1+r
2 ⇒ Okręgi te przecinają się w dwóch punktach

12 maj 22:14
żwirek:
S1 = (−2, 2), r1 = 2, S2 = (−5, 2), r2 = √25 + 4 − 25 = 2,
d = |S1S2| = √9 + 0 = 3, r1 + r2 = 4, |r1 − r2| = 0
|r1 − r2| < d <r1 + r2, okręgi maja 2 punkty wspólne
12 maj 22:14
Nel: okręgi rozłączne zewnętrznie
12 maj 22:18
żwirek:
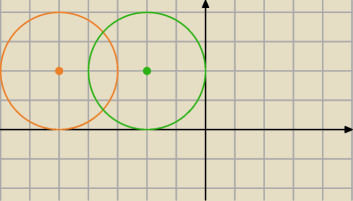
12 maj 22:27
muchomorek:

12 maj 22:40
Nel: czy aby na pewno to jest dobrze? Wydaje mi się, że te okręgi mają być rozłączne zewnętrznie
12 maj 23:42
mały książę:
To uzasadnij, ze okręgi są rozłączne, a jak nie potrafisz, to się nie odzywaj
12 maj 23:48
chichi:
A to dopiero ciekawe

13 maj 00:04
Rumcajs:
a więc
Nel nie potrafisz

13 maj 01:25
Ola: no właśnie też ktoś podał odpowiedź, że to okręgi rozłączne i mam dojść do rozwiązania
13 maj 05:56




