planimetria jendrzej: Dany jest trójkąt prostokątny 𝐴𝐵𝐶. Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta 𝐴𝐵𝐶, który ma większą miarę

	a+b−c		c		a+b−c		7c		7
r=				=				=a+b/:c sinα+cosα=		/2
	2		5		2		5		5

	49		24		24
sin2α+2sinαcosα+cos2α=		2sinαcosα=		2sinαsinβ=
	25		25		25

	12
sinαsinβ=		brakuje mi puenty
	25

janek191:

	24
2 sin α*cos α =		/ : 2
	25

	12
sin α* √1 − sin2α=		podnosimy do kwadratu
	25

	144
sin2α*(1 − sin2α) =
	625

sin²α = t 0 < t < 1

	144
t*(1 − t) =
	625

	144
− t2 + t −		= 0
	625

	144
t2 − t =		= 0
	625

	49
Δ =
	625

	7
√Δ =
	25

	9		16
t =		lub t =
	25		25

	9		16
sin2 α =		lub sin α =
	25		25

	3		4
sin αα =		lub sin α =
	5		5

Bierzemy większy kąt, więc

	4
Odp.		.
	5

jendrzej: Dzięki janek191:

figa:

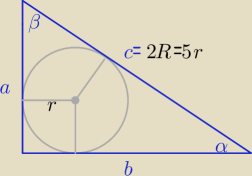
	a		b		7
a+b=2r+2R ⇒ a+b=7r / :5r ⇒		+		=
	5r		5r		5

	7
to sinα+cosα=		|2
	5

	24		24		7
2sinαcosα=		⇒ sin2α=		to cos2α=
	25		25		25

ze wzoru cos2α=1−2sin²α

	7		3
to 2sin2α= 1−		⇒ sinα=
	25		5

	4
zatem sinβ= cosα=
	5

=============

Hubert888: A skąd wiemy że taki trójkąt nie będzie trójkątem prostokątnym równoramiennym

an: czy nie prościej z Pitagorasem obwód to 2*5+2*1=12 a+b+5=12 a=7−b a²+b²=5² b₁=3 a₁=4 b₂=4 a₂=3 większy kąt leży naprzeciw większego kąta

	4
sinα=
	5

. : Hubert, początkowo nie wiemy, ale to nie zmienia sposobu rozwiązania @an − a na jakiej podstawie zakładasz r=1

an: czego nie wiemy ? r=1 czyli jedna jednostka długości c=5*r=5 czyli pięć jednostek długości źle napisałem oczywiście powinno być większy kąt leży naprzeciw większego boku

wredulus_pospolitus: @an ... 'nie wiemy' odnosiło się do Hubertowego pytania odnośnie tego czy taki trójkat może być trójkątem prostokątnym równoramiennym. ponownie −−− PRZYJMUJESZ sobie r = 1, co oczywiście można zrobić ... natomiast gdybyś tak napisał na maturze to powinni (ale pewnie by tego nie zrobili) za to obciąć punkty.

an: Ja pokazałem, że zadanie może rozwiązać osoba nie znająca trygonometrii. Nie mogą być równe co wyraźnie widać, z wyników można to także potwierdzić przy pomocy wzoru na promień okręgu wpisanego, a także robiąc rysunek i zauważając, że

	5
√2 + 1<		, trzeba tylko trochę chcieć.
	2

Nie podlegam Twojej ocenie na maturze, którą zdawałem z pradziadkami większości tu piszących. Kiedyś dyskutowaliśmy o gotowcach, ja tu i tak za dużo napisałem uczeń powinien dostać tylko wskazówki, a dokładniejszą podpowiedź na zadane przez niego pytanie.

Mila: Do sposobu an, wystarczy dodać komentarz, że podobieństwo nie zmienia wartości funkcji trygonometrycznych.

wredulus_pospolitus: @Miluś ... albo po prostu wszędzie pisać 'r' które i tak będzie się skracać przy ułamkach.

Mila: Ja piszę r , ale to więcej rachunków Pozdrawiam z wielkanocnymi życzeniami: WESOŁYCH ŚWIĄT !

Mila:

Mariusz:

	2P
r =
	a+b+c

	1
P =		bc sin(α)
	2

bcsin(α)
	= r
a+b+c

r(a+b+c) = bcsin(α)

	r(a+b+c)
sin(α) =
	bc

	r(a+b+5r)
sin(α) =
	b*5r

	(a+b+5r)
sin(α) =
	5b

	1		a		5r
sin(α) =		(		+ 1 +		)
	5		b		b

	1		1
sin(α) =		(tg(α) + 1 +		)
	5		cos(α)

	1
5sin(α) = tg(α) + 1 +
	cos(α)

5sin(α)cos(α) = sin(α)+cos(α) + 1 (sin(α)+cos(α))² = sin²(α)+2sin(α)cos(α) + cos²(α) (sin(α)+cos(α))² = 1 + 2sin(α)cos(α) 2sin(α)cos(α) = (sin(α)+cos(α))² − 1

5
	((sin(α)+cos(α))2 − 1) = sin(α)+cos(α) + 1
2

sin(α)+cos(α) = t

5		5
	t2 −		= t + 1
2		2

5t² − 5 = 2t+2 5t² −2t − 7 =0

	2±12
t =
	10

	7		4
t =		∨ t = −
	5		5

	7
sin(α)+cos(α) =
	5

	1		1		7
√2(cos(α)*		+sin(α)*		) =
	√2		√2		5

	π		7
√2cos(α−		) =
	4		5

	π		7
cos(α−		) =
	4		5√2

	π		7√2
cos(α−		) =
	4		10

	π		7√2
α−		= arccos(		)
	4		10

	π		7√2
α =		+ arccos(		)
	4		10

	π		7√2
sin(α) = sin(		+ arccos(		))
	4		10

	√2		7√2		√2		7√2
sin(α) =		cos(arccos(		))) +		sin(arccos(		)))
	2		10		2		10

	√2		7√2
sin(α) =		(		+ √1−98/100)
	2		10

	√2		7√2		√2
sin(α) =		(		+		)
	2		10		10

	√2		8√2		16		4
sin(α) =		*		=		=
	2		10		20		5

M:

Mariusz:

	2±12
t=
	10

	7
t =		∨ t = −1
	5

	7
Z t =		mamy dwie możliwości
	5

	π		7√2
α1 =		+ arccos(		)
	4		10

	π		7√2
α2 =		− arccos(		)
	4		10

t = −1 należy odrzucić , rozwiązania nie będą spełniać warunków zadania w dodatku jedno z rozwiązań będzie rozwiązaniem obcym powstałym z obustronnego przemnożenia równania przez cos(α)